Vliv třídy rozdělení časových odstupů na kapacitu neřízených křižovatek
Rubrika: Doprava
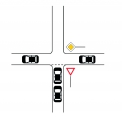
Při výpočtu kapacity neřízených křižovatek se v současnosti hojně využívá metoda kritických časových odstupů, která je v tuzemsku rovněž východiskem příslušných technických podmínek. Metoda se začala rozvíjet už v polovině minulého století a lze ji demonstrovat na jednoduchém modelu křížení dvou jednopruhových komunikací na obr. 1 [1].
Základem metody je jednoduchá úvaha, že vznikne-li na hlavní komunikaci dostatečně dlouhá časová mezera mezi následně jedoucími vozidly, vozidlo z vedlejší komunikace se stihne mezi ně zařadit. Zmíněné časové mezery (tzv. časové světlosti) ovšem mají, jak je zřejmé, stochastickou povahu, a jakožto náhodné veličiny jsou tudíž příslušně statisticky rozděleny. Běžně se předpokládá, že světlosti mají exponenciální rozdělení pravděpodobnosti, které odpovídá známému Poissonovu rozdělení výskytu vozidel v určitém časovém intervalu. Postupem času tuto základní teorii rozvinula celá řada dalších prací [2, 3], až vznikla dnes nejrozšířenější podoba definovaná Brillonem ve tvaru
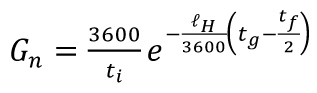 (1)
(1)
kde Gn je základní kapacita n-tého jízdního proudu, IH rozhodující intenzita nadřazených dopravních proudů, tg je kritický časový odstup a tf je následný časový odstup.
Ve všech přístupech je nicméně zachován základní předpoklad exponenciálního rozdělení pravděpodobnosti časových světlostí. V reálných dopravních systémech ale tento předpoklad není naplněn téměř nikdy s výjimkou extrémně nízkých hustot dopravního proudu. Skutečné chování dopravního systému je tomuto předpokladu vzdáleno tím více, čím větší je jeho hustota [4, 5, 6]. Je proto zřejmé, že je nutné výše uvedený přístup revidovat, k čemuž lze s výhodou využít současných empirických znalostí o rozděleních časových světlostí a jejich závislostech na dopravní hustotě. Za vhodné alternativy k nesprávně užívanému exponenciálnímu rozdělení lze považovat gamma rozdělení [7], log-normální rozdělení [8, 9], nebo inverzní Gaussovo rozdělení [5, 10].
EXPONENCIÁLNÍ ROZDĚLENÍ SVĚTLOSTÍ – APARÁT TECHNICKÝCH PODMÍNEK
Rovnice definované Brillonem a použité v německé normě Handbuch für die Bemessung von Straßenverkehrsanlagen (HBS) [11] přejímají i české normativy včetně exponenciálního rozdělení pravděpodobnosti výskytu časových mezer odvozeného z předpokladů platných pro tzv. poissonovské systémy vzájemně neinteragujících elementů. Tyto rovnice jsou uváděny jako obecné a platné za všech podmínek. Jak však uvádí Medelská [12], toto rozdělení, popsané matematicky vztahem
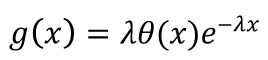 (2)
(2)
kde λ > 0 je parametr související se střední hodnotou světlosti a θ (x) Heavisideova funkce (θ (x) = 1 pro x > 0 a θ (x) = 0 pro x ≤ 0), je platné pouze při splnění následujících tzv. Adamsových‑Kinzerových kritérií:
a) vozidla udržují v dopravním proudu různé časové odstupy, které jsou závislé na hustotě a rychlosti dopravního proudu,
b) všechna vozidla se mohou pohybovat volně, nezávisle na sobě a předjíždění je vždy možné,
c) průjezd vozidla sledovaným profilem je náhodný,
d) pravděpodobnost výskytu časového odstupu dané délky ve zvoleném časovém intervalu je přibližně úměrná jeho délce.
Je zřejmé, že tyto předpoklady platí pouze omezeně a zejména bod b) platí jen ve fázi volného dopravního proudu, což zpravidla není ten případ, kdy kapacitu křižovatek řešíme. Rovněž platnost bodů c) a d) je pro vysoké hustoty přinejmenším diskutabilní. Jak se ukazuje, sousední světlosti jsou výrazně korelovány a úměra popsaná v posledním bodě ve skutečnosti vykazuje extrémní fluktuace [13]. Pokud tedy zamýšlíme teoretické předpovědi kapacit křižovatek přiblížit realitě, je nezbytné stávající vzorce inovovat. A změna rozdělení pravděpodobnosti světlostí je poměrně jednoduchým a efektivním krokem, jak toho dosáhnout.
ROZDĚLENÍ SVĚTLOSTÍ V REÁLNÉM PROVOZU
Za rozdělení světlostí alternativní k exponenciálnímu lze, jak již bylo zmíněno, považovat tzv. gamma distribuci
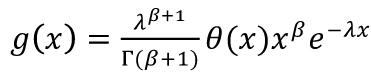 (3)
(3)
nebo zobecněné inverzní Gaussovo rozdělení (GIG)
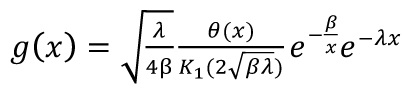 (4)
(4)
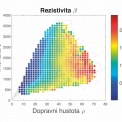
kde Km (y) je Macdonaldova funkce řádu m. V obou případech se jedná o dvouparametrickou třídu distribucí, v níž lze hodnotu λ kalibrovat na reálnou střední hodnotu světlostí. Hodnota β (tzv. statistická rezistivita) je pak v souladu s aktuálními výsledky výzkumu závislá na hodnotě dopravní intenzity a hustoty (viz obr. 2) [14].
Na základě známých hodnot intenzity J a hustoty ϱ lze tedy pro daný dopravní vzorek určit nejen hodnotu rezistivity, ale rovněž hodnotu škálovací konstanty λ. Tím je příslušný tvar rozdělení světlostí určen jednoznačně.
KAPACITA KŘIŽOVATKY
Kapacita křižovatky přímo souvisí s hodnotou pravděpodobnosti, že se v hlavním proudu vyskytne mezi vozidly časová mezera větší, než je kritická hodnota potřebná k zařazení vozidla z vedlejší komunikace na hlavní. Jinými slovy to znamená, že rozhodující veličinou pro průjezd vozidla je pravděpodobnost P[NT = 0], že se během kritického času T nevyskytne v bodě křížení komunikací žádné vozidlo. Jako příklad použijeme hodnotu T = 3,6 s, která je uvedena v TP 234 pro jednopruhové okružní křižovatky s velkou vzdáleností vjezdů a výjezdů, což je přijatelná aproximace základní úlohy z obr. 1. Hodnota P[NT = 0] ale bezprostředně souvisí s tvarem distribuce g(x),
a sice podle vztahu
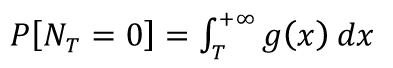 (5)
(5)
Je-li tedy g(x) volena nesprávně, bude se skutečná pravděpodobnost velmi pravděpodobně lišit od teoreticky vypočtené hodnoty P[NT = 0] (viz obr. 3 a 4). Na první pohled je totiž zřejmé, že pokud přijmeme současný normativ jako východisko, pak bude hodnota P[NT = 0] zohledňovat pouze intenzitu (která ovlivňuje střední hodnotu časové světlosti), ale na hustotě dopravy nijak záviset nebude. Kapacita křižovatky se ale zcela jistě s hustotou mění. Proto je nezbytné přejít k výpočtu hodnoty P[NT = 0] za použití současných znalostí z oblasti statistiky dopravní mikrostruktury.
SROVNÁNÍ JEDNOTLIVÝCH VARIANT
Chceme-li porovnat, jak se současná metodika stanovování kapacity křižovatky odchyluje od reálných hodnot kapacity, lze k tomu elegantně využít srovnání hodnot PEXP [NT = 0] a PGIG [NT = 0] (popřípadě PΓ [NT = 0]) vyčíslených za předpokladu distribucí světlostí exponenciálních, GIG nebo gamma. Takové srovnání lze provádět pro dopravní vzorek pohybující se zvolenou rychlostí v uvnitř dopravního proudu o hustotě ϱ. Na základě volby těchto dvou veličin lze snadno dopočíst hodnotu intenzity J = ϱv, z ní zase střední hodnotu světlostí μ = 3 600 / J. Pro variantu exponenciálně distribuovaných světlostí je tím jednoznačně určen parametr λ, neboť
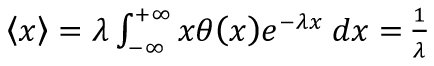 (6)
(6)
odkud λ=1/μ. Volíme-li jako výchozí distribuci gamma rozdělení, pak je nejprve nutno na základě hodnot hustoty a intenzity stanovit konkrétní hodnotu rezistivity β (viz obrázek 2), a poté kalibrovat hodnotu druhého parametru λ za použití rovnosti středních hodnot
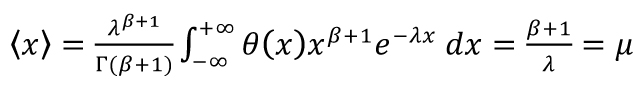 (7)
(7)
Analogicky postupujeme pro GIG distribuci, kde
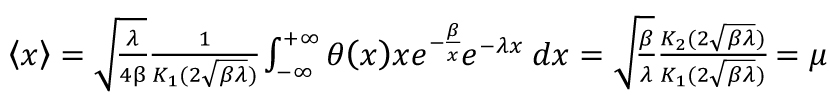 (8)
(8)
Jsou-li nyní oba parametry kalibrovány, lze pro vybraná hustotní a rychlostní pásma vyčíslovat chybu, které se dopouštíme, přebíráme-li hypotézu, že se výskyty vozidel na vozovce řídí Poissonovým rozdělením. Výsledek takového srovnání je dobře patrný na obrázku 4, kde vidíme, že chyba klasického přístupu může činit až poměrně vysokých 15 %.
ZÁVĚR
V předchozích částech textu jsme ukázali, že použití exponenciálního rozdělení světlostí v kapacitních výpočtech není při současných matematických poznatcích opodstatněné a je dáno spíše historicky. Rovněž se nabízí do kapacitních výpočtů zahrnout hustotu dopravního proudu, která, na rozdíl od intenzity, lépe vystihuje jeho stav
a schopnost pojmout nebo propustit další vozidla. To by sebou sice na jedné straně přineslo zvýšené nároky na měření dopravního proudu a jisté zvýšení komplexnosti výpočtů, na straně druhé je však značný potenciál pro jejich zpřesnění.
Autoři: doc. Mgr. Milan Krbálek, Ph.D., Ing. Jiří Apeltauer, doc. Mgr. Tomáš Apeltauer, Ph.D.
Příspěvek vznikl za podpory projektu GA15-15049S, financovaného Grantovou agenturou České republiky, a projektu č. LO1408 „AdMaS UP – Pokročilé stavební materiály, konstrukce a technologie“ podporovaného Ministerstvem školství, mládeže a tělovýchovy v rámci účelové podpory programu „Národní program udržitelnosti I“.
Recenzent:
Ing. Bc. Petr Kumpošt, Ph.D.,
ČVUT v Praze, Fakulta dopravní
LITERATURA:
[1] Grabe, W. Leistungsermittlung von nicht lichtsignalsteuerten Knotenpunkten des Straßenverkehrs [Capacity calculation of unsignalized intersections in road traffic]. (Forschungsarbeiten aus dem Strassenwesen, Neue Folge 11). Bielefeld: Kirschbaum Verlag (1954).
[2] Harders, J. Die Leistungsfähigkeit nicht signalgeregelter städtischer Verkehrsknoten. Straßenbau und Straßenverkehrstechnik, Vol. 76, Bonn: Federal Ministry of Transport (1968).
[3] Siegloch, W. Die Leistungsermittlung an Knotenpunkten ohne Lichtsignalsteuerung. Straßenbau und Straßenverkehrstechnik, Vol. 154, Federal Ministry of Transport, Bonn (1973).
[4] Helbing, D. Traffic and related self-driven many-particle systems, Rev. Mod. Phys. 73, 1067 (2001).
[5] Krbalek, M., Helbing, D. Determination of interaction potentials in freeway traffic from steady-state statistics, Physica A 333 (2004) 370 – 378.
[6] Krbalek, M., Equilibrium distributions in thermodynamical traffic gas, J. Phys. A: Math. Theor. 40 (2007), 5813 – 5821.
[7] Krbalek, M, Seba, P., Wagner, P. Headways in the traffic flow – remarks from a physical perspective, Phys. Rev. E 64 (2001), 066119 – 066125.
[8] Li L., Chen X., Vehicle headway modeling and its inferences in macroscopic/microscopic traffic flow theory: A survey, Transportation Research Part C, 76 (2017) 170 –188.
[9] Přibyl, P., Mach, R., Řídicí systémy silniční dopravy, skripta ČVUT FD, Praha, 2003.
[10] Krbalek, M., Equilibrium distributions in thermodynamical traffic gas, J. Phys. A: Math. Theor. 40 (2007), 5813 – 5821.
[11] Handbuch für die Bemessung von Straßenverkehrsanlagen: HBS, FGSV-Verlag, 2005, ISBN 9783937356440.
[12] Medelská, V., Jirava, P., Nop, D., Rojan, J. Dopravné inžinierstvo. 1. vyd. Alfa Bratislava, 1991, 376 s.
[13] Krbálek, M., Quantitative analysis of interaction range in vehicular flows, Transportation Research Procedia 25 (2017) 1268 – 1275.
[14] Krbalek, M., Hobza, T., Inner structure of vehicular ensembles and random matrix theory, Physics Letters A 380/21 (2016) 1839 – 1847.
When calculating the capacity of uncontrolled intersections, there is widely used method of critical time gaps. These time gaps has a stochastic nature and as random variables are therefore appropriately statistically distributed. It is commonly assumed these gaps have an exponential probability distribution that corresponds to a known Poisson distribution of vehicle occurrence within a certain time interval. In real transport systems, however, this assumption is almost never fulfilled, except for extremely low traffic flow densities. We show in this paper that as suitable alternatives can be considered Gamma distribution, log-normal distribution or inverse Gaussian distribution.











![Obr. 3a – Srovnání pravděpodobnosti výskytu časové mezery P[NT = 0] pro exponenciální rozdělení (červeně) (rovnice 2) a GIG rozdělení (modře) (rovnice 4). Grafy jsou vyneseny pro rychlost v = 40 km/h. Hustota provozu je volena ϱ = 20 voz/km.](/PublicFiles/UserFiles/image/SZ/2017/SZ417/122x122_apt03a.jpg)
![Obr. 3b – Srovnání pravděpodobnosti výskytu časové mezery P[NT = 0] pro exponenciální rozdělení (červeně) (rovnice 2) a GIG rozdělení (modře) (rovnice 4). Grafy jsou vyneseny pro rychlost v = 40 km/h. Hustota provozu je volena ϱ = 50 voz/km.](/PublicFiles/UserFiles/image/SZ/2017/SZ417/122x122_apt03b.jpg)
![Obr. 4 – Chyba stanovení hodnoty P[NT = 0] při použití exponenciálního rozdělení hustoty pravděpodobnosti (rovnice 2) ve srovnání s GIG rozdělením hustoty pravděpodobnosti (nulová hladina) (rovnice 4).](/PublicFiles/UserFiles/image/SZ/2017/SZ417/122x122_apt04.jpg)







