Stanovení interakční vzdálenosti vozidel z empirických dat

Tento problém se snažil vyřešit Luise A. Pipes a v roce 1953 publikoval svoji práci Operational Analysis of Traffic Dynamics [9] ve které položil základy mikroskopických modelů dopravního proudu. Pipesův model pracoval s interakcemi mezi jednotlivými (po sobě následujícími) vozidly, a měl tedy potenciál popsat chování dopravního proudu v dosud nevídané přesnosti. Bohužel tento model neměl analytické řešení a numerické řešení bylo vzhledem k úrovni a ceně dobových počítačů velice omezené, v běžné praxi prakticky nemožné. Postupem času vznikaly různé modifikace Pipesova přístupu, základní mechanizmus však zůstal stále stejný: na základě rychlosti, případně zrychlení vedoucího vozidla a časového kroku se mění rychlost vozidla následujícího (tzv. car‑following modely). Toto zjednodušení je zcela legitimní a podává přijatelné výsledky, avšak je zřejmé, že v reálném provozu jsou interakce mezi jednotlivými vozidly složitější a více vzdálené. Pokud tedy chceme modely dopravního proudu dále zpřesňovat, musíme definovat interakční vzdálenost mezi vozidly a intenzitu této interakce.

ČASOVÉ ODSTUPY VOZIDEL

Interakce mezi vozidly (jak blízké tak vzdálené) lze měřit jen obtížně. Je sice možné udělat měření se speciálně vybavenými vozidly [2] nebo využít analýzu videa [3], avšak těmito přístupy vždy získáme velice omezený vzorek dat. Chceme‑li interakce studovat s využitím stávající senzoriky instalované na pozemních komunikacích – což je jediný způsob jak můžeme získat dostatečně rozsáhlý datový vzorek – musíme hledat veličiny a postupy, které nám umožní interakce mezi vozidly studovat nepřímo. Jednou z možností je sledování časových odstupů mezi vozidly, které je možné se stávající technikou měřit velice přesně a bylo prokázáno, že prostřednictvím této veličiny lze sledovat celou řadu vlastností mikrostruktury dopravního proudu [1][4].

Pod pojmem časový odstup vozidel v tomto případě myslíme čistý časový odstup (time clearance – časovou mezeru mezi vozidly) a označíme jej tc_n. Vzdálenost mezi sousedními vozidly označíme jako n = 0 pro interakci mezi vozidly k a k – 1 (obr. 1), kdy n + 2 je počet vozidel a n + 1 počet mezer. Obecně tedy pracujeme s časovým odstupem mezi vozidly podle vztahu:

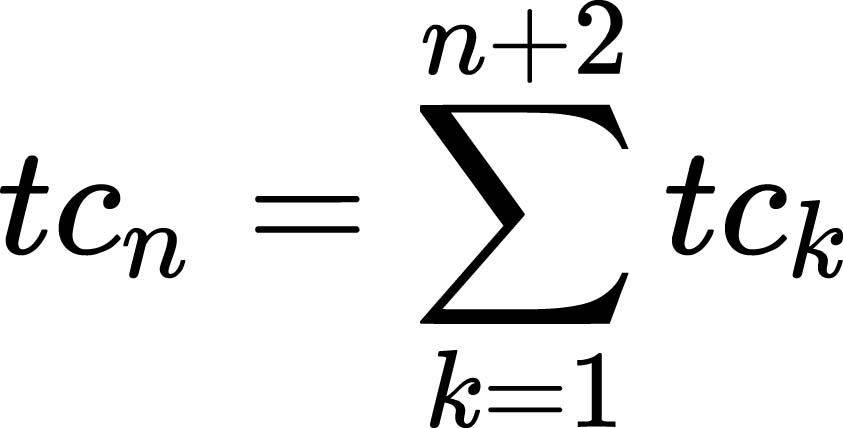
MATEMATICKÉ A STATISTICKÉ NÁSTROJE

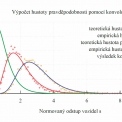
Dopravní proud je ze své podstaty nestabilní a je tedy překvapivé, že existuje podobnost mezi chováním dopravního proudu a termodynamického plynu. Krbálek však v několika pracích tuto závislost prokázal a definoval rozdělení hustoty pravděpodobnosti GIG – Generalized Inverse Gaussian distribution [7], které velice přesně aproximuje hustotu pravděpodobnosti časových odstupů mezi vozidly. Definování a hlavně ověření platnosti GIG je pro další rozvoj v oblasti teorie dopravního proudu klíčovým krokem, jelikož otevírá široké možnosti dalšího zkoumání dopravního proudu prostřednictvím nepřímých měření s využitím statistických a matematických nástrojů.

V problematice interakční vzdálenosti vozidel tak můžeme využít operaci konvoluce:

s jejíž pomocí je možné spočítat kombinovanou hustotu pravděpodobnosti dvou nezávislých veličin. Známe‑li tedy teoretickou hustotu pravděpodobnosti ρ (s) pro n = 0 a pro n, můžeme pomocí konvoluce spočítat teoretickou hustotu pravděpodobnosti pro n + 1 (obr. 2). Bude‑li se teoretická hustota pravděpodobnosti pro n + 1 statisticky lišit od empirické hustoty pravděpodobnosti pro n + 1, zamítáme nulovou hypotézu, že časové odstupy n a n + 1 jsou statisticky nezávislé veličiny, což může být důsledkem interakce mezi příslušnými vozidly.

ODHAD INTERAKČNÍ VZDÁLENOSTI

K ověření nulové hypotézy můžeme použít například Kolmogorovův‑Smirnovův test [6]:

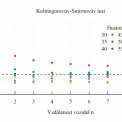
který sleduje maximální odchylku dvou funkcí. Kritická hodnota D_krit je závislá na počtu měření. V našem případě jsme vyhodnocovali datový vzorek v rozsahu cca 3,2 milionu měření, pořízený na části dálniční sítě. Tento vzorek byl rozdělen na 8 hustotních pásem v rozmezí 25 – 70 voz/km po 5 voz/km. V jednotlivých hustotních pásmech byla data dále rozdělena na bloky 5 000 měření, pro které D_krit = 0,0272. Výsledek analýzy je vidět na obr. 3, kde je vykreslen průměr hodnot D_n, jelikož pro jednotlivá hustotní pásma bylo více bloků 5 000 měření.

ZÁVĚR

Popsaný postup umožňuje prokázat, že předpoklady použité v současné teorii dopravního proudu a v tzv. car‑following modelech nejsou zcela přesné, tedy že chování řidiče je ovlivněno nejméně dvěma předcházejícími vozidly, v některých případech však i 4 až 5 vozidly (u nižších hustot). Tento výsledek podporují i další metody uvedené v [6] a rovněž je toto chování povědomé samotným řidičům. Pro n = 1 (dvě mezery a tři vozidla na obr. 1) byla kritická hodnota překročena ve všech případech, vyjma hustoty 60 – 65 voz/km, která je hraniční a tudíž zamítáme nulovou hypotézu v důsledku interakce mezi příslušnými vozidly.

Dopad tohoto zjištění však nemá uplatnění pouze v teorii dopravního proudu a dopravních modelech, ale je možné jej aplikovat i v oblasti autonomních vozidel, jejichž řízení je často založeno na chování předcházejícího vozidla. Než však bude možné závislosti popsané v této práci uvést do praxe, je nutné zodpovědět otázku, jak je celková interakční síla mezi vzdálenější vozidla rozdělena.

Autor:
Ing. Jiří Apeltauer,
doc. Mgr. Tomáš Apeltauer, Ph.D.
Vysoké učení technické v Brně, Fakulta stavební

Recenzent:
Ing. Bc. Petr Kumpošt, Ph.D.,
ČVUT v Praze, Fakulta dopravní

LITERATÚRA:
[1] Krbálek, M.; Apeltauer, J.; Apeltauer, T. Analýza mikrostruktury dopravního proudu s využitím standardních empirických dat. Silnice a železnice, 2016, roč. 2016, č. 5, s. 20 – 22. ISSN: 1801‑822X.
[2] Apeltauer, T.; Macur, J.; Holcner, P.; Radimský, M. Validation of Microscopic Traffic Models Based on GPS Precise Measurement of Vehicle Dynamics. PROMET– Traffic & Transportation, 2013, roč. 25, č. 2, s. 157 – 167. ISSN: 0353‑5320.
[3] Apeltauer, J.; Herman, D.; Babinec, A.; Apeltauer, T. Automatic Vehicle Trajectory Extraction for Traffic Analysis from Aerial Video Data. In ISPRS Archives. Mnichov: Technische universität münchen, 2015. s. 9 – 15. ISSN: 2194‑9034.
[4] Krbálek, M.; Apeltauer, T.; Apeltauer, J.; Všetečka, M. Analýza mikrostruktury dopravního proudu metodami teorie náhodných matic. Silnice a železnice, 2015, roč. 2015, č. 2, s. 77 – 79. ISSN: 1801‑ 822X.
[5] Apeltauer, J. Statistické vlastnosti mikrostruktury dopravního proudu, Disertační práce, Brno 2017 
[6] Krbálek, M.; Apeltauer, J.; Apeltauer, T.; Szabová, Z. Three methods for estimating a range of vehicular interactions. Physica A, 2017, roč. 2018, č. 491, s. 112 – 126. ISSN: 0378‑4371.
[7] Krbálek, M.; Hobza, T.: Inner structure of vehicular ensembles and random matrix theory. Physics Letters A, roč. 380, č. 21, 2016: s. 1839 { 1847, ISSN 0375‑9601.
[8] Greenshields B. D., B. J. R.: A Study Of Traffic Capacity. Proceedings of the Fourteenth Annual Meeting of the Highway Research Board Held at Washington, D.C. December 6 – 7, 1934, roč. 1, 1935: s. 448 – 477. URL https://trid.trb.org/view.aspx?id=120649
[9] Pipes, L. A.: An Operational Analysis of Traffic Dynamics. Journal of Applied Physics, roč. 24, 1953: str. 274.

Příspěvek vznikl za podpory projektu GA15‑15049S, financovaného Grantovou agenturou České republiky, a projektu č. LO1408 „AdMaS UP – Pokročilé stavební materiály, konstrukce a technologie“ podporovaného Ministerstvem školství, mládeže a tělovýchovy v rámci účelové podpory programu „Národní program udržitelnosti I“.

Determination of the Interaction Distance between Vehicles Based on Empirical Data
Interaction between vehicles can be difficult to measure. While it is possible to measure with specially equipped vehicles or use video analysis, we always get a very limited sample of these data. If we want to study interactions using existing detection equipment – which is the only way we can get a sufficiently large data sample – we need to look for variables and procedures that allow us to study interactions between vehicles indirectly. One possibility is to measure the time differences between vehicles, which can be obtained with sufficient precision with the existing technique. Presented paper demonstrate the possibility to measure a number of properties of the traffic flow microstructure.

Autoři

• Ing. Apeltauer Jiří
• doc. Mgr. Apeltauer Tomáš Ph.D.