Modelování dynamiky dopravního proudu

ÚVOD
Náš příspěvek je strukturován následovně. Nejprve se zaměříme na matematické modelování dopravního toku, které vychází ze zákona zachování na základě podobnosti s proudem tekutiny a řadí se do kategorie makromodelů. Model je charakterizován hustotou, tokem a rychlostí dopravního proudu a lze jej popsat pomocí parciálních diferenciálních rovnic 1. řádu. Obsahem 2. kapitoly článku je stručné odvození tohoto modelu, popis základních pojmů a vysvětlení způsobu, jakým je řešení rovnice – určení hustoty dopravního toku v daném čase a místě – prezentováno. Třetí kapitola přináší popis způsobu řešení na základě multiagentního přístupu k modelování daného problému. Ve 4. kapitole je zařazen popis počátečních podmínek, který byl zvolen tak, aby odpovídal realitě zpracovávané v obou pohledech, dále následuje shrnutí výsledků experimentu. V 5. kapitole je provedena analýza dosažených výsledků a 6. kapitola představuje závěr článku. Cílem je potvrdit naše výzkumné očekávání shody výsledků obou experimentů a porovnat klady a zápory použitých modelů.

MATEMATICKÝ MODEL
Hustota a tok aut
Pohyb vozidel na silnici lze popsat analogicky jako proudění tekutiny s tím rozdílem, že vyjádření závislosti toku na hustotě bude odlišné. Tok vozidel na silnici je možné chápat z jistého úhlu pohledu a za daných podmínek jako tok částic tekutiny (např. při pohledu na silnici z letadla). Pohyb částic tekutiny je ovlivňován pohybem okolních částic, ovšem jízda řidiče závisí i na jiných faktorech. Řidič přizpůsobuje jízdu podle rozumové úvahy situaci před sebou či za sebou a vnímá další faktory, které mohou rozhodnout o změně jeho jízdy či rychlosti jeho jízdy. Částice tekutiny se může při svém pohybu srazit s jinou částicí, řidič vozidla se srážce s jiným vozidlem samozřejmě vyhýbá. Protože vozidla budou v našem modelu představovat jednotky, budeme předpokládat, že mají totožnou délku. Dále předpokládejme pro zjednodušení, že se vozidla pohybují konstantní rychlostí pouze jedním směrem a nepředjíždějí se. Pro určení počtu vozidel na měřeném úseku za danou časovou jednotku musíme vzít v úvahu jednak celkovou hustotu vozidel a jejich rychlost. Hustotu vozidel definujeme následovně:

hustota vozidel = počet vozidel / jednotková délka silnice

a dále v textu ji budeme označovat symbolem ρ. V případě ρ = 0 je měřený úsek silnice prázdný. Hustotu vozidel budeme určovat v daném místě x a v daném čase t a budeme ji zapisovat jako funkci dvou reálných proměnných ve tvaru ρ (x, t), kde t ≥ 0 a x ϵ R. Předpokládejme, že na daném úseku je dána maximální rychlost, označme ji v_max. Pak lze vyjádřit závislost rychlosti na hustotě následovně viz [5]²:

kde ρ_max je hustota, při níž dochází k zácpě a ρ ≤ ρ_max.

Dalším důležitým pojmem určujícím charakter silničního provozu je tok vozidel daný vztahem:

tok vozidel = počet vozidel / čas.

Tok vozidel můžeme definovat mnoha způsoby, nejjednodušší cestou je chápat tento pojem jako součin hustoty vozidel a rychlosti, jíž se vozidla pohybují. Pokud v textu zavedeme jednotné označení pro rychlost vozidel symbolem a pro funkci toku vozidel symbolem φ, pak platí:


V případě, že se ve sledovaném úseku bude rychlost vozidel měnit v závislosti na podmínkách na silnici například při nehodě vozidel či na základě příkazu omezené rychlosti nebo reakce na světelnou signalizaci, nebude toková funkce lineární funkcí a bude záviset na dalších parametrech (maximální rychlost vozidel, maximální hustota vozidel). Při volbě závislosti φ na ρ dané vztahem (2) lze tokovou funkci přepsat následovně:


Předpokládejme, že každé vozidlo má délku 4,5 m a při jízdě za sebou dodržují řidiči bezpečnostní vzdálenost, tedy časový odstup 2 s. V případě, že vozidla jedou rychlostí 50 km/h, jedná se o úsek dlouhý 28 m. V případě, kdy se na úseku silnice dlouhém 1 000 m vyskytuje maximálně 200 vozidel, jedná se o zácpu.

Model dopravního toku
Sledujme v daném časovém intervalu úsek silnice, na kterém se vozidla pohybují konstantní rychlostí v a hustota vozidel ρ je v daném úseku a čase zadána. Základní úvaha pro sestavení rovnice závislosti rozložení hustoty vozidel na daném úseku na čase a místě spočívá v tom, že změna počtu vozidel na měřeném úseku za danou časovou jednotku je totožná s rozdílem mezi počtem vozidel, které do uvažovaného úseku vjedou a vyjedou. Tedy změna hustoty provozu v čase t je totožná se změnou tokové funkce v měřeném úseku. Určíme-li počet vozidel v čase t = t₀ = 0 a v čase t = t₁ ≥ 0, pak jejich rozdíl bude představovat změnu hustoty vozidel zjištěnou v čase t = t₁. Spočteme-li vozidla, která za čas t1 do měřeného úseku rychlostí v vjedou a současně vyjedou, pak určíme změnu tokové funkce měřené v daném místě. Tuto závislost lze přepsat do podoby parciální diferenciální rovnice 1. řádu ve tvaru:


kde symbolem p_t resp. [φ(ρ)]_x značíme 1. parciální derivaci funkce ρ (x, t) podle proměnné t resp. 1. parciální derivaci funkce φ (ρ) podle proměnné x viz [3]. Rovnici (4) dále můžeme přepsat do tvaru:

přičemž ρ_x je 1. parciální derivace funkce ρ (x, t) podle proměnné x.

V případě, kdy toková funkce φ(ρ) je zadána v lineárním tvaru jako v (2), přechází rovnice (4) do tvaru:


Konkrétní řešení dané úlohy (rozložení hustoty vozidel v určitém čase a místě) budeme moci určit, jakmile budeme znát rozložení hustoty vozidel v daném místě a čase. Nejčastější a nejpřirozenější volbou podmínek bývá počáteční rozložení hustoty vozidel, tedy popis situace na začátku sledovaného děje ve tvaru³:


kde funkce ρ₀ (x) popisuje funkci ρ (x, t) v čase t = 0. V případě volby tokové funkce ve tvaru (3) lze odvodit následující vztah:


Metoda charakteristik
Jedním ze způsobů popisu řešení úlohy je cesta grafického znázornění pomocí charakteristických přímek. Rovnice (6) s počáteční podmínkou ρ (x, 0) = ρ₀ (x) má jednoduchý tvar, a proto lze řešení snadno uhodnout. Hledaná funkce ρ proměnné x a t ≥ 0 má tvar:


Body na přímkách se směrnicí rovnou v ve tvaru:


mají společnou vlastnost. Funkce ρ je v bodech všech přímek se směrnicí v konstantní. Tyto přímky se nazývají charakteristické přímky nebo charakteristiky příslušné k dané úloze. Zakreslit charakteristiky je snadné a pomocí výsledného grafického znázornění pak můžeme získat řešení dané úlohy v předem určeném čase a místě. Význam charakteristik zůstává nezměněn i v případě, kdy řešíme nelineární úlohu (5). Charakteristiku pak definujeme jako přímku se směrnicí φ'(ρ₀) rovnou ve tvaru:


kde t_ρ0 je bod, ze kterého odpovídající charakteristika vychází. Na této přímce je hodnota řešení ρ (x, t) rovna odpovídající hodnotě počáteční podmínky ρ (x, 0) viz [3].

Složitější situace nastává v případě, kdy je úloha s počátečním rozložením hustoty zadána následovně:


kde ρ_p a ρ_l jsou daná nezáporná čísla⁴. Zde pak mohou nastat dvě rozdílné situace viz [4]:

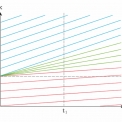
1. ρ_l < ρ_p

Charakteristiky pro hodnotu ρ_l znázorníme červenou barvou a charakteristiky pro hodnotu ρ_p vykreslíme modrou barvou. V prázdné oblasti definované nerovností ρ_l t < x < ρ_p t, charakteristiky „chybí“. Zakreslíme-li charakteristiky se směrnicemi mezi hodnotami ρ_l a ρ_p (zelenou barvou), doplníme informaci o hodnotě přenášené hustoty v oblasti skoku (vlna zředění) viz obr. 1.

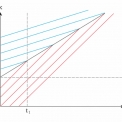
2. ρ_l > ρ_p

V tomto případě se charakteristiky budou křížit. Směr, ve kterém se bude z prvních průsečíků charakteristik přesouvat informace o skoku (rázová vlna), je dán tzv. Rankine-Hugoniotovou podmínkou viz [3] ve tvaru:


Na obr. 2 je znázorněna přechodová linie. V čase t₁ je pak řešení úlohy snadno čitelné.

Pokud budeme uvažovat tokovou funkci ve tvaru (3), pak rychlost šíření nespojitosti daná Rankine-Hugoniotovou podmínkou lze vyjádřit vztahem viz [5]:

SIMULAČNÍ MODEL
Popis modelu
Druhý zkoumaný a užitý přístup k návrhu modelu dopravního toku je multiagentní, chování skupiny vozidel bude modelováno jako agregace chování jednotlivých vozidel viz [2]. I zde je nutné využít určitá data (parametry) popisující systém jako celek, je však možné individuálně modelovat chování každého vozidla. Výhodou tohoto přístupu může
pro řadu uživatelů být i fakt, že znalost výše zmíněných parciálních diferenciálních rovnic a práce s nimi není pro tento typ modelu vyžadována – na úrovni modelování jednotlivých vozidel nebudou pro popis systému nutné. Globálními parametry jsou v tomto případě povolená rychlost v jednotlivých úsecích a frekvence výskytu vozidel, která byla nastavena na pevnou hodnotu 1 vozidlo za 3 s. Dalším globálním parametrem je pak délka vozidla stanovená na 4,5 m a minimální vzdálenost od vozidla bezprostředně před vozidlem zkoumaným stanovená na 0,5 m. Výše uvedená frekvence výskytu vozidel tak odpovídá hustotě 0,021 vozidel/m při maximální rychlosti 50 km/h.

Konceptuální model úlohy vychází z modelování vozidla jako samostatného agenta a jeho umístění do prostředí sledovaného úseku komunikace. Po svém vstupu do prostředí je agent inicializován a umístěn na pozici danou buď vstupními podmínkami nebo (pro čas t > 0) na počátek modelovaného úseku (x = 0 m). Agent si také při své inicializaci ukládá informaci o agentovi bezprostředně před ním, aby jej mohl kontaktovat při zjišťování vzájemné polohy a vzdálenosti mezi vozidly. Při inicializaci je také nastaven cílový bod, do kterého se agent má dostat, tedy konec modelovaného úseku.

Další chování agenta je modelováno pomocí stavových diagramů a jeho hlavní činností je pohyb po modelovaném úseku komunikace, přičemž v pravidelných intervalech (v modelu je použito 0,05 s modelového času) agent kontroluje svou vzdálenost od vozidla (agenta) před ním. Při této kontrole je zásadní, zda tato vzdálenost není menší, než vzdálenost bezpečná pro danou rychlost, která (vyjádřená v čase) činí 2 s. Pokud je vzdálenost menší, agent na tento stav reaguje úpravou své rychlosti tak, aby vzdálenost bylo možné považovat opět za bezpečnou. Pokud je vzdálenost mezi vozidly dostatečná, agent nastaví svou rychlost na maximální povolenou hodnotu v daném úseku. Ke zpracování dat a znázornění výsledků byl využit softwarový program AnyLogic [1].

PROVEDENÉ EXPERIMENTY
Počáteční podmínky
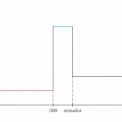
Sledovaný úsek komunikace o délce 1 000 m je rozdělen na tři části: 0 – 500 m s maximální rychlostí 50 km/h, vozidla zde dodržují bezpečnostní vzdálenost 2 s, úsek 500 – 600 m s maximální hustotou vozidel simulující kolonu před semaforem (maximální rychlost 0 km/h) a úsek 600 – 1 000 m s maximální rychlostí 30 km/h. Počáteční podmínka je zadána v 1. úseku hodnotou ρ₁ = 0,021 vozidel/m (červená barva), ve 2. úseku ρ₂ = 0,2 vozidel/m (modrá barva) a v posledním úseku je počáteční hodnota hustoty dána hodnotou ρ₃ = 0,046 vozidel/m (černá barva) viz obr. 3. V čase t = 0 s se na semaforu rozsvítí zelená barva a vozidla se začnou rozjíždět.

Grafické výsledky
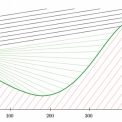
V první části vyřešíme danou počáteční úlohu z makroskopického úhlu pohledu. Zpracujeme veškeré informace dané počátečními podmínkami dle postupu uvedeného v kapitole 2. Vykreslíme-li všechny odpovídající charakteristiky a určíme-li pomocí Rankine-Hugoniotovy podmínky dle vztahu (15) směry, jimiž se šíří jednotlivé nespojitosti, pak získáme podrobný přehled o situaci na sledované vozovce v závislosti na měnícím se čase viz obr. 4.

Z grafu lze určit přibližné hodnoty času a místa, ve kterém dochází ke změnám v toku dopravního proudu. V místě, kde se protíná červená charakteristika se zelenou charakteristikou přenášející v součtu hodnotu hustoty přibližně rovnou 0,2 vozidel/m, je směrnice přechodové linie rovná nule (k tomuto stavu dochází přibližně v čase 180 s v místě přibližně 160 m od startu). V čase zhruba 360 s již auta nejsou omezována a mohou volně projíždět kolem semaforu.

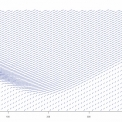
V případě druhého multiagentního přístupu se výsledný graf konstruoval následovně. Počáteční podmínka byla nastavena tak, že ve všech třech úsecích bylo vygenerováno a rozmístěno právě tolik agentů, kolik odpovídalo maximální rychlosti v úseku. Čas t₀ = 0 modelového času byl nastaven pro okamžik, kdy na semaforu umístěném v místě vzdáleném 600 m od počátku (před kolonou ve druhém úseku komunikace) naskočí zelená. Výsledky provedené simulace byly vizualizovány ve dvou rovinách. Prvním výstupem je tak graf v systému souřadnic t – x, ukazující polohu každého z agentů v konkrétním čase (obr. 5) a jeho aktuální rychlost (směrnice úsečky v daném bodě). Na tomto grafu je velmi dobře viditelný přechodový děj, který proběhne při rozjezdu kolony ve druhém úseku. Hustota čar ve svislém směru zde ukazuje na hustotu vozidel na celé komunikaci v zadaném čase, ve vodorovném směru pak můžeme sledovat časový vývoj děje v konkrétním místě (vývoj rychlosti vozidel v tomto místě). Graf byl aktualizován s frekvencí 7 s. V levé části obrázku je pro názornost zobrazena schematicky celá trasa s polohou vozidel.

Z grafu je možné odečíst několik klíčových hodnot. Předně je možné sledovat proces rozjíždění kolony stojící před semaforem. Z grafu lze odhadnout, že poslední vozidla se rozjela teprve přibližně 120 s po změně barvy semaforu na zelenou. Zpomalení vozidel však pokračovalo i nadále a nejhorší situace nastala v čase t = 200 s, kdy se začátek
omezení rychlosti vozidel posunul do místa x = 165 m od počátku sledovaného úseku. Přechodový děj pak odezněl v čase t = 432 s, přičemž nadále se již projevila pouze snížená rychlost v posledním úseku sledované trasy.

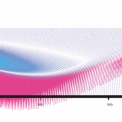
Pro větší názornost uvedeného děje byl vytvořen také 3D graf uvedený na obr. 6. Ten znázorňuje vývoj změny (diference) rychlosti v čase pro každé vozidlo. Záporné hodnoty diference rychlosti (zpomalení) jsou uvedeny červeně se sytostí odpovídající intenzitě uvedeného jevu, naopak při zrychlení jsou použity odstíny zelené. Okamžiky a místa s malou změnou rychlosti jsou v odstínech modré. Z grafu je dobře patrné i trvalé snížení rychlosti na začátku posledního úseku sledované trasy po odeznění přechodového děje.

POROVNÁNÍ VÝSLEDKŮ
Hlavním cílem našeho příspěvku bylo porovnání dvou metod popisu dynamiky dopravního toku za daných počátečních podmínek. Výstupy jsou pak zachyceny na obrázcích 4, 5 a 6. Z grafů je patrné, že výstupy obou modelů jsou velmi podobné. Základem pro toto konstatování je především minimální odchylka v pozicích klíčových bodů uvedených v popisu jednotlivých experimentů. Odlišnost je patrná pouze v čase ukončení přechodového děje, kde byl matematický makromodel optimističtější, než model multiagentní, což logicky plyne z nezahrnutí přechodových jevů. Je tedy možné formulovat závěr, že oba modely popsaly zvolený přechodový děj minimálně se lišícími kvantitativními hodnotami, čímž byla potvrzena hlavní hypotéza, kterou měl náš příspěvek ověřit.

Při porovnání experimentálních výsledků je nutné mít na paměti různý charakter obou modelů (makroskopický a mikroskopický). Matematický makroskopický model nemá možnost zachytit přechodový jev v takové míře detailu a je zde nutné řešit problém nespojitostí počáteční podmínky pomocí (15). Pro detailní zkoumání přechodového jevu je
evidentně vhodnější model mikroskopický, který je však výpočetně náročnější. Po vytvoření modelu je možné jej však využít s relativně malými obměnami pro simulaci i jiných stavů systému.

ZÁVĚR
V našem příspěvku jsme se soustředili na porovnání dvou způsobů modelování dynamiky dopravního toku. Porovnávány byly simulační multiagentní model a matematický model založený na řešení parciální diferenciální rovnice. Ačkoliv se principy obou modelů výrazně liší, je z výsledků experimentů zřejmé, že modely jsou ve svých výstupech
porovnatelné, detailnější výsledky poskytuje (v souladu s předpoklady) model simulační, který je však na druhou stranu náročnější na výpočetní kapacity. Na závěr lze tedy konstatovat, že experimentální porovnání obou modelů potvrdilo, že pro simulování přechodových dopravních dějů lze využít oba přístupy s obdobnými výsledky, avšak s různými postupy a výpočetní náročností.

Recenzovala: doc. Ing. Bibiána Buková, Ph.D.

REFERENCE:
[1] AnyLogic Company, 1992–2012. AnyLogic. [Online] Available at: http://www.anylogic.com [Accessed 2. 11. 2012]
[2] Siebers, P. O. &Aickelin, U., 2008. Introduction to Multi-Agent Simulation. In: F. Adam & P. Humphreys, eds. Encyclopedia of Decision Making and Decision Support Technologies. Pennsylvania: Idea Group Publishing, pp. 554–564
[3] LeVeque R.: Finite Volume Methods for Hyperbolic Problems, Cambridge University Press 2002, pp. 203–213. ISBN 0521009243
[4] Lustri, Ch.: Continuum Modelling of traffic Flow. Available at http://people.maths.ox.ac.uk/lustri/Traffic.pdf
[5] Hokr, M.: Transportní procesy. Učební text, Technická univerzita v Liberci, 2005, pp. 77–84

Poznámky:
1 – Článek byl vytvořen s podporou interních grantů č. 1/2012 a č. 3/2013 při Vysoké škole technické a ekonomické v Českých Budějovicích
2 – Model navržený matematiky Lighthillem, Whithamem a Richardsem v roce 1955
3 – Úloha je známá pod názvem počáteční úloha (Cauchyho úloha)
4 – Tato úloha se nazývá Riemannova úloha

Traffic Flow Dynamics Modelling
The work’s aim is to compare results of two completely different approaches to traffic flow dynamics modelling. The traffic system modelling method is affected by many factors. The crucial role here is played by data availability for given modelling method and naturally also the required level of detail. Therefore, we distinguish two basic groups of models. First group is represented by macromodels focusing on system’s overall behaviour and requiring global entry data (an example can be the use of principles of system dynamics). The opposite are micromodels specialising in detailed description of behaviour of model’s individual elements.

Autoři

• Ing. Jelínek Jiří CSc.
• RNDr. Vysoká Jana