Analýza mikrostruktury dopravního proudu metodami teorie náhodných matic

Zvyšující se intenzity dopravního proudu, nedostatečná kapacita komunikací, rostoucí emise skleníkových plynů a související dopady představují značný problém ve většině rozvinutých i dosud se rozvíjejících zemí. Z toho důvodu také tyto státy, především USA a Evropská unie, investují značné prostředky do problematiky dopravního výzkumu. Současně se ukazuje, že problémy optimálního řízení dopravy jsou (kromě jiných faktorů) způsobené také postupným a nevyhnutelným zastaráváním nástrojů užívaných pro dopravní modelování, kdy dva v současnosti nejrozšířenější nástroje v sobě integrují matematické modely dopravního proudu z šedesátých, resp. osmdesátých let minulého století.

Jedním z příspěvků, který má ambici situaci na poli dopravních modelů zlepšit, je letos zahájený projekt podporovaný Grantovou agenturou České republiky s názvem „Detekce stochastických univerzalit v nerovnovážných stavech sociofyzikálních systémů metodami teorie náhodných matic“ a řešený ve spolupráci Českého vysokého učení technického, Fakulty jaderné a fyzikálně inženýrské, a Vysokého učení technického v Brně, Fakulty stavební.

ÚVOD DO PROBLEMATIKY
Pokud se podíváme na pohyb libovolné dostatečně velké skupiny lidí nebo zvířat, objeví se před námi řada prvků samostatné vědní disciplíny zvané skupinová dynamika. Pro účely našeho projektu tyto „skupiny“ chápeme jako samoorganizované systémy, jejichž jednotlivé prvky (tzv. agenti) jsou ovlivňovány ostatními agenty v okolí [1]. V praxi to znamená, že každý jednotlivý agent uzpůsobuje svoje chování zbytku skupiny, přičemž tyto interakce jsou logicky spíše krátkého dosahu, tedy omezeny na agenty v nejbližším okolí. Chování pohybujících se agentů dále doplňují externí a interní faktory, mezi které řadíme např. individualitu agenta nebo stochastické vlivy apod. Typickým kolektivním chováním takové množiny agentů je pak tendence vytvářet samoorganizované shluky, v rámci kterých je chování jednoho agenta velmi silně korelováno s ostatními.

Výše popsané chování je dopravním inženýrům velmi známé z reálného chování dopravního proudu, který má sklon přecházet mezi třemi různými stavy – volným, metastabilním a synchronizovaným dopravním proudem či dopravní kongescí. Popsané stavy lze snadno identifikovat pomocí nejrozšířenějšího prostředku používaného pro popis dopravního proudu, tzv. fundamentálního diagramu. Používá se pro popis globálních vlastností ustáleného dopravního proudu a jeho nejčastější varianta zachycuje závislost intenzity dopravního proudu q(x,t) na hustotě ρ(x,t), která je jednoznačně stanovená následujícím vztahem


kde v(x,t) je střední rychlost vozidel v dopravním proudu a všechny veličiny jsou funkcí polohy a času.

Je tedy zřejmé, že vzájemné individuální interakce mezi agenty na mikroskopické úrovni vedou ke změnám v dynamice systému jako celku a tedy ke změně makroskopických veličin systému. Dále platí, že makroskopické vztahy popisující globální chování dopravního systému významně ovlivňují jeho mikroskopickou strukturu, která má statistickou povahu generovanou individualitou každého z agentů. Zatímco ve volném dopravním proudu můžeme detekovat pravděpodobnostní rozdělení odpovídající čisté nahodilosti, v případě kongesce je systém výrazně ovlivněn silnými psychologickými interakcemi, které nahodilost potlačují a vedou k výrazným změnám struktury celého systému. V současné době jsou tyto mikroskopické vlastnosti měřitelné [2, 3, 4], což otevírá nové možnosti jejich výzkumu v rámci řešeného projektu.

ZÁKLADY AGENTNÍHO MODELU
V rámci řešeného projektu zavádíme zobecněný agentní model, jehož vlastnosti jsou v dobré shodě s chováním, které běžně pozorujeme u dopravního či pěšího proudu [5].

Model si lze představit jako kouli, na jejímž povrchu (nebo jeho vymezené části) se pohybují částice – agenti. Poloha každého agenta s indexem i je definována vektorem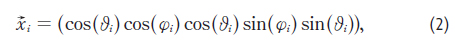

kde úhly ν_i a φ_i představují standardní komponenty sférických souřadnic.

Zároveň platí, že vzájemné interakce mezi agenty jsou krátkého dosahu, tedy každý jednotlivý agent interaguje pouze s agenty ve svém blízkém okolí, které označujeme jako f. Tuto interakci lze popsat následujícím způsobem

kde V(r_ik) odpovídá silovému potenciálu mezi dvěma tělesy v závislosti na jejich obecné vzdálenosti

Tato interakce odpovídá realistickému chování elementů dopravního či pěšího proudu a mimo jiné splňuje základní předpoklad bezesrážkovosti, tedy

Energie souboru (tzv. hamiltonián) je potom popsána jako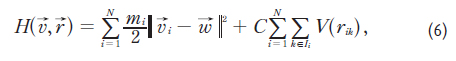

kde první část výrazu představuje analogii s kinetickou energií bodu s hmotností m_i a C je kalibrační konstanta. Druhá část výrazu zachycuje schopnosti jednotlivých agentů se vzájemně přitahovat či odpuzovat, což reflektuje reálné chování řidičů v dopravním proudu, kteří mění akceleraci vozidla v závislosti na relativní rychlosti k vozidlům ve svém okolí (především k předcházejícímu vozidlu). Tento model lze pro konkrétní praktické simulace redukovat na jedno- či dvourozměrné oblasti pro modely vozidel či pěších, funguje tedy velmi dobře jako obecný koncept.

TERMODYNAMICKÉ ROZŠÍŘENÍ ZÁKLADNÍHO MODELU
Výše popsaný model je striktně deterministický a jak jsme uvedli již na počátku, deterministický popis není schopen plně obsáhnout reálné vlastnosti dopravního či pěšího proudu. Z toho důvodu je model rozšířen o termodynamickou alternativu [6], která základní model vystaví „lázni“ o předem dané teplotě T, čímž jsou zajištěny náhodné fluktuace agentů v souladu se statistickými vlastnostmi jejich reálného chování. Rozšíření modelu lze provést prostřednictvím termální komponenty

kde k_B je Boltzmannova konstanta a parametr b lze chápat jako kvantitativní analogii k psychickému stresu, kterému je vystaven pohybující se řidič či chodec.

Implementací tohoto rozšíření původně čistě deterministického systému jsme získali soubor, jehož ustálený stav lze popsat statisticky. Sledujeme tedy mikroskopické veličiny v ustáleném stavu (odstupy vozidel prostorové i časové, jejich rychlosti apod.) pomocí odpovídajících rozdělení (hustot) pravděpodobnosti.

Cíle řešeného projektu jsou následující:

• dokázat, že statistické rozdělení termálního systému analyzovaného mimo rovnovážný stav odpovídá za určitých okolností ustálenému stavu s jiným nastavením parametrů,
• ukázat, že popsaný systém lze interpretovat jako zvláštní případ tzv. Dysonova plynu, který je propojen s novou třídou náhodných matic,
• nalézt tuto novou třídu náhodných matic, jejichž spektrum vlastních hodnot vykazuje vlastnosti podobné dynamickým charakteristikám proudu vozidel.

První snaha o nalezení této třídy „dopravních náhodných matic“ již byla zveřejněna dříve [7] a představuje revoluční, hojně citovanou možnost propojení náhodných matic s matematickými strukturami teorie dopravního proudu.

PŘEDSTAVENÍ PROBLEMATIKY TEORIE NÁHODNÝCH MATIC
Teorie náhodných matic byla v padesátých letech minulého století vyvinuta prioritně pro účely statistického popisu komplexních (zejména kvantových) systémů. Na přelomu tisíciletí se ale ukázalo, že prediktivní potenciál teorie je mnohem pestřejší. Mezi oblasti, v nichž lze náhodné matice (tj. matice s elementy vybranými z jistých tříd náhodných rozdělení) s úspěchem uplatnit, patří také oblast dopravního proudění. Jestliže budeme na dopravní systém nahlížet jako na stochastický soubor vozidel interagujících prostřednictvím obtížně detekovatelných interakcí, lze jej v první fázi zjednodušit do systému bodových částic vzájemně propojených jistými blíže nespecifikovanými silami, jejichž účinky se vzrůstající vzdáleností klesají. Řešit takový systém pak znamená predikovat jeho chování bez znalosti konkrétních interakčních vzorců. Nalezením příslušných řešení a metodikou komparace výstupů s reálnými systémy se zaobírá právě teorie náhodných matic.

Pro konkrétní představení aplikace teorie náhodných matic lze s výhodou užít následující schéma. Budeme-li uvažovat jednorozměrný řetězec částic propojených vzájemně pružinami o tuhostech, jejichž velikost je náhodnou veličinou, lze řešení takového systému převést na hledání spektra náhodné matice obsahující zmíněné náhodné tuhosti. Ustálený stav systému (tj. např. statistické rozložení poloh, vzdáleností nebo frekvencí kmitů) je pak přímo propojen s uspořádáním vlastních čísel ve spektru náhodné matice. Klesají-li střední hodnoty tuhostí se vzdáleností mezi elementy, máme před sebou jednoduchý model dopravního působení, jehož náhodná matice má tu specifickou vlastnost, že její elementy jsou tlumeny koeficientem úměrným vzdálenosti od diagonály. Jaké vlastnosti taková třída má? Čím se liší od klasických tříd „netlumených“ náhodných matic? Proč lze takového schématu užít k modelování dopravy? To jsou otázky, na které bude hledat citovaný projekt odpovědi.

AKTUÁLNÍ VÝSLEDKY PROJEKTU A JEHO SHRNUTÍ
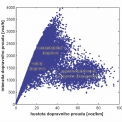
V první fázi projektu je třeba bezpodmínečně odstranit vágnosti dopravního popisu, které fyzika dopravního proudění aktuálně užívá. Nejzřetelnější z nich je patrná již při samotném procesu oddělování dopravních fází. Jelikož teorii náhodných matic má smysl aplikovat pouze na synchronizovaný dopravní režim (neboť ve volném režimu se systém chová jako poissonovský), je nezbytné volné a synchronizované stavy dopravy matematicky separovat. K tomuto účelu lze s výhodou použít a) statistickou metodu tzv. k-středování (K-means, viz [8]) a b) metodu analýzy tzv. brownovské distanční kovariance [9]. Kombinací těchto metod lze (po eliminaci oblastí s lineární závislostí dopravního toku na hustotě) získat poměrně přesný přehled o úrovni korelací mezi za sebou jedoucími vozidly. Přitom čím je taková korelace vyšší, tím je míra synchronizace v systému intenzivnější (kongestivní stavy) a naopak. Z barevné reprezentace hladiny brownovské distanční kovariance (viz obr. 3) je dobře patrné, kde se ve fundamentálním diagramu nacházejí kongestivní oblasti a kde naopak dochází vlivem zřeďování systému k rozvolňování původně intenzivní synchronizace.

Jak už bylo popsáno výše, projekt je zaměřen na analýzu matematických a statistických vlastností mikrostruktury dopravního a pěšího proudu, přičemž navazuje na dosavadní vysoce citovanou práci části řešitelského týmu v této oblasti. Výsledkem projektu bude nový a zároveň dostatečně ucelený přístup k analýze dopravy s využitím již existujících detekčních zařízení, které umožní vytvoření efektivnějších systémů řízení dopravy a pěších ve spolupráci s aplikační sférou a Ředitelstvím silnic a dálnic ČR.

LITERATURA:
[1] H. Moon, D. E. Conlon, S. E. Humphrey, N. Quigley, C. E. Devers, and J. M. Nowakowski, Organizational Behavior and Human Decision Processes 92 (2003), 67
[2] C. Appert-Rolland, Phys. Rev. E 80 (2009), 036102
[3] M. Krbálek, J. Phys. A: Math. Theor. 41 (2008), 205004
[4] M. Krbálek and P. Šeba, J. Phys. A: Math. Theor. 42 (2009), 345001
[5] M. Krbálek, J. Phys. A: Math. Theor. 40 (2007), 5813
[6] D. Helbing, M. Treiber, and A. Kesting, Physica A 363 (2006), 62
[7] E. Bogomolny, O. Giraud and C. Schmit, Nonlinearity 24 (2011), 3179
[8] J. A. Hartigan, Clustering algorithms, John Wiley & Sons, Inc. (1975)
[9] G. J. Szekely and M. L. Rizzo, Annals of Applied Statistics 3/4 (2009), 1236

Článek vznikl za podpory grantu č. 15-15049S poskytnutého Grantovou agenturou České republiky a projektu specifického výzkumu Fakulty stavební VUT v Brně FAST-S-15-2933.

Recenze: Ing. Zuzana Švédová, Ph.D.

Analysis of Microstructure of Traffic Stream by Method of Accidental Matrix Theory
Natural sciences like presenting themselves as islands of rational thinking in today’s postmodern world. Nevertheless, even they do not avoid certain superstitions. A belief that a good mathematical model of any given system which accurately describes its properties, makes reliable prediction of the future development of the system as a whole possible, can be considered to be one of these chimeras of natural sciences. Even today, some people believe that an accurate model of the world, which is perfectly predictable thanks to accurate knowledge of the initial conditions, can be constructed on the basis of these simple principles. The first scientific discipline, which definitely refused this initial idea, was quantum mechanics. However, the fact that this idea is actually completely groundless has been becoming more obvious to most of the scientific fields including transport during the last decades.

Autoři

• doc. Mgr. Apeltauer Tomáš Ph.D.
• Ing. Apeltauer Jiří
• Ing. Všetečka Martin
• doc. Mgr. Krbálek Milan Ph.D.