Ověření některých modelů dopravního proudu

• Foto

VÝCHOZÍ PODMÍNKY
Jednou z nejvýraznějších vlastností tzv. euroatlantické civilizace, ve které žijeme, je tendence k růstu. Míra růstu (ekonomiky, populace, produkce, spotřeby…) je považována zároveň za míru úspěchu a musíme připustit, že v tomto ohledu je naše společnost dlouhodobě úspěšná. Relativně krátká a málo častá období poklesu jsou označována za krizi. V dopravě převažuje například znepokojení z lednového poklesu mýta o pětinu nad běžnými obavami ze „závodění kamiónů“ na přecpané dálnici. Ale osobní zkušenost podepřená statistickými daty nás přesvědčuje, že dlouhodobým spolehlivým trendem v dopravě je růst. V tomto oboru však, právě asi kvůli přímé osobní zkušenosti, vnímáme více než v ekonomické oblasti problémy, které přináší naplňování teze úspěšného růstu. V každém případě je však jasné, že růst dopravy, kýžený nebo trpěný, vyžaduje plánování, predikci a prognózy a hlavním prostředkem k tomu jsou simulace a modelování [1].

DOSTUPNÉ NÁSTROJE PRO MODELOVÁNÍ
Modelování dopravního proudu má hodně společného s předpovídáním počasí. Jde o komplexní děje, které mají nelineární dynamický charakter. Předpovědi jsou založeny na matematickém modelu a obecně platí, že více vstupních dat a větší výpočetní výkon může přinést větší přesnost. Závislost mezi množstvím zpracovaných podkladů a kvalitou výsledku však není v žádném případě lineární a je všeobecně známou skutečností, že víceparametrické nelineární dynamické systémy jsou z principiálních důvodů nepředvídatelné. Libovolně malá změna vstupních údajů totiž může vést k zásadně odlišnému výsledku.

Existuje však jeden velký rozdíl mezi předpověďmi počasí a dopravním modelováním, a to v tradici těchto činností. Zájem o počasí provází lidstvo po celou historii. Historie modelu dopravního je samozřejmě kratší, auta se vyrábějí až od začátku dvacátého století, a teprve problémy s jejich přebytkem na silnicích byly důvodem k úvahám o dějích v dopravním proudu. Jedním z důsledků překotného růstu automobilizmu (a problémů s ním) a krátké historie vědeckého zkoumání je to, že nedošlo zatím ke všeobecné shodě o dějích v dopravním proudu, tím méně ke shodě s realitou.

Pro posouzení dopravních komunikací a sítí a pro predikce dějů se běžně používají simulační softwarové balíky, výsledky z nich získané se považují za dostatečně spolehlivé a relevantní – především na úrovni makroskopické, tedy v hromadných a shrnujících výsledcích, jako jsou intenzity a rychlosti dopravních proudů. Pokusili jsme se ověřit jejich věrohodnost na úrovni mikroskopické, tedy při zkoumání dějů zjistitelných u jednotlivých simulovaných vozidel. Předpokládáme, že pochopení zákonitostí mikroskopických dějů a jejich věrohodný popis je předpokladem pro efektivnější modelování praktických problémů.

Zkoumali jsme dva často používané (v komerčních programových balících) modely z kategorie tzv. psycho-fyziologických – Wiedemannův a Fritzscheho model a porovnávali je s modelem z kategorie modelů optimální akcelerace postaveným na základě Treiberova modelu IDM (Intelligent Driver Model), který dlouhodobě zkoumáme a rozvíjíme na našem pracovišti. Pro jejich porovnání s reálným dopravním proudem jsme uskutečnili měření v dopravním proudu na třech vozidlech, jejichž polohy jsme určovali za pohybu pomocí GPS přístrojů s fázovým měřením metodou RTK. Použité přístroje a metody zpracování dat umožnily dostačující přesnost měření do 1 cm při frekvenci 10 měření za sekundu. V obr. 1 je patrné uspořádání pokusu a zároveň i označování vozidel používané v modelech.

Základem mikroskopických modelů je obecně předpis pro určení akcelerace (kladné či záporné) v každém okamžiku v závislosti na nejbližším okolí:

Slovně vyjádřeno – akcelerace vozidla (reakce vozidla na sešlápnutí plynu nebo brzdy) závisí na vzájemné pozici blízkých vozidel a na jejich rychlostech. Většinou se za rozhodující považuje vlastní rychlost vozidla, rozdíl rychlostí vzhledem k předcházejícímu vozidlu a vzdálenost od předcházejícího vozidla.

REŽIM SLEDOVÁNÍ
Pro psycho-fyziologické modely se berou do úvahy tři stavové charakteristiky – vzdálenost od předcházejícího vozidla, rozdíl rychlostí vzhledem k předcházejícímu vozidlu a vlastní rychlost vozidla. To se běžně demonstruje na grafu, ve kterém se vynáší vzdálenost mezi vozidly a rozdíl rychlostí, a v grafu jsou definovány různé předpokládané stavy s různými reakcemi řidiče. Vykreslené hranice vymezující různé stavy jsou však závislé na rychlosti vozidla. Uvedený graf definuje oblasti pouze pro jednu konkrétní rychlost (viz obr. 2 platný pro Wiedemannův model), pro jiné rychlosti platí grafy obdobné ale s modifikovanými mezemi. Fritzscheho model používá obdobný postup, jen jinak definuje meze a má i odlišné předpisy pro stanovení akcelerace. Podrobný popis obsahující definice hranic jednotlivých jízdních režimů je dostupný v odborné literatuře [2] a [3].

Oba uvedené modely však shodně předpokládají, že při optimální kombinaci rychlosti, rozdílu rychlostí a rozdílu vzdáleností je vozidlo v režimu sledování a setrvává v něm, pokud nedojde ke změně stavových charakteristik (prakticky to znamená – dokud předcházející vozidlo nezmění rychlost. Oba modely se však snaží respektovat empiricky zjištěné kolísání rychlosti vozidel předpisem pro jízdu v režimu sledování tím, že udržují nenulovou akceleraci např. v rozmezí ±0,1 ms^–2. Ke střídání akcelerace a decelerace dochází při dosažení hranice oblasti sledování. Oblast sledování se uvažuje relativně malá – viz obr. 2. Předpokládaný režim sledování autoři většinou znázorňují v grafech, u kterých se předpokládá hladký a spojitý průběh tak, jak je naznačeno v obr. 3.

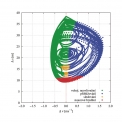
Uvedený předpoklad jsme se pokusili ověřit měřením reálných vozidel v dopravním proudu. Naše měření ukázalo podstatně větší kolísání vzdáleností a hlavně větší rozdíly rychlostí, režim sledování nenastával. Typický průběh vztahu rozdíl rychlostí – vzdálenost naměřený na reálných vozidlech je patrný v obr. 4 a odpovídá dostupným měřením jiných autorů [4]. Změřené a vynášené hodnoty jsou vyhodnoceny podle Wiedemannových kritérií a v obrázku jsou odlišeny barevně odpovídající stavy vozidla. Pouze malá část měření byla vyhodnocena do oblasti sledování (oranžová barva) a vozidla v tomto stavu nesetrvávala.

Převládal volný režim (zelená) a režim přibližování (modrá). Překvapivě velká část stavů je podle Wiedemanna vyhodnocena jako režim nouzového brzdění (červená barva). Velmi jednoduchým a názorným způsobem ověření je simulace jízdy za vedoucím vozidlem jedoucím konstantní rychlostí. Kromě předpokládaných oscilací akcelerace v režimu sledování v hodnotách ±0,1 m . s^–2 nastávají nespojité fluktuace akcelerace na hodnotu +1,0 m/s² při krátkodobém přechodu do režimu neovlivněného pohybu. Ty zjevně odporují realitě a jsou zdrojem nestability, pokud uplatníme model na větší počet vozidel v simulovaném dopravním proudu.

Obdobné, ale méně podrobné výsledky jsou dostupné v odborné literatuře [5]. Přirozeným rozšířením pokusu je přidání dalšího vozidla. Ukazuje se, že předpoklad režimu sledování není naplněn a zvýrazňuje se nespojitý průběh akcelerace. V obr. 5 je vykreslený vztah rozdílu rychlostí a vzdáleností pro druhé vozidlo podle Wiedemanna za prvním Wiedemannovým vozidlem z obr. 4. Je zjevné, že režim sledování není dodržen, vozidlo z něj vypadává především do režimu přibližování a do volného režimu. Každá taková změna je doprovázena nespojitým průběhem akcelerace.

SIMULACE NA OKRUHU
Další rozšíření počtu vozidel jsme prováděli na simulované kruhové dráze s 250 identickými vozidly. Pro funkční model je oprávněný požadavek na bezkolizní a stabilní vývoj dopravního proudu, vzhledem k výše popsaným nespojitostem však toho nebylo možné dosáhnout ani pro Wiedermannův, ani pro Fritzscheho algoritmus. Dobrých výsledků jsme dosáhli s modelem IDM, který dlouhodobě ověřujeme. Mimo jiné jsme jej implementovali do simulačního programu, ve kterém se velký počet vozidel (v řádu stovek) autonomně pohybuje po kruhové dráze (typicky o poloměru 1 000 m). Algoritmus IDM (dostupný i v českých v odborných časopisech [6]) je poměrně jednoduchý a účinný – důležité je, že průběh akcelerací je spojitý v souladu s empirií. Splňuje dobře základní požadavky kladení na modely dopravního proudu:

• bezkoliznost prováděných simulací v celém spektru možných parametrů a počátečních podmínek,
• fyzikálně rozumné hodnoty rychlostí a zrychlení vozidel v průběhu simulace,
• asymetričnost modelu – průběh akcelerace odlišný od decelerace (obvykle je přípustná razantnější decelerace např. v případě hrozící kolize),
• vznik globálních stavů odpovídajících reálnému pozorování
  – nelinearita modelu (vlny stop and go, spontánní vznik kongescí při nadkritických hustotách, hystereze intenzity dopravního proudu při nadkritické a podkritické hustotě apod.).

Prokázal se spontánní vznik nehomogenit (vzdálenosti mezi vozidly a rychlosti se v čase a po dráze mění) i pro identická simulovaná vozidla. V zobrazené simulaci (obr. 6) jsme vyhodnocovali stavy vozidel podle Wiedemannových kritérií – jsou opět barevně odlišeny stejně jako v obr. 4. Ani tento pokus s identickými vozidly neprokázal tendence modelu IDM k setrvání v režimu sledování (žlutá barva). Většinu času se vozidlo nachází ve volném režimu (zelená barva) nebo v režimu přibližování (modrá barva). Menší rozptyl rychlostí ve srovnání s reálnými vozidly lze vysvětlit tím, simulovaná vozidla měla nastavenu neměnnou požadovanou rychlost, zatímco při pokusu s reálnými vozidly vedoucí vozidlo rychlost záměrně měnilo.

PRAKTICKÉ DŮSLEDKY
Pokud zkoumáme modely dopravního proudu, které jsou deklarovaným základem používaných programových prostředků, nacházíme zjevné rozpory s realitou ale i se samotnými výchozími předpoklady těchto modelů. Režim sledování tak, jak jej modely definují, není udržitelný ani při konstantní rychlosti vedoucího vozidla a při počtu pouhých dvou následujících vozidel. Přesto jsou tyto modely používány a jejich výsledky jsou přijímány jako věrohodné. To můžeme vysvětlovat dvěma skutečnostmi:

• Autoři těchto modelů se zajímali pouze o celkové, makroskopické, hromadné výsledky, které mají praktické užití. Především tedy o střední intenzity a rychlosti dopravního proudu. Chování jednotlivých vozidel a shoda s realitou na mikroskopické úrovni pro ně nebyla důležitá. Simulování konkrétních dopravních situací (vjezd do křižovatky, předjíždění, změna jízdního pruhu, spojování  dopravních proudů) je obvykle implementováno pomocí ad hoc pravidel, která nemusejí nutně odpovídat reálným možnostem simulovaného vozidla. Model je pak navíc zpětně kalibrován podle statistických výsledků simulace tak, aby odpovídal empirickým hodnotám. Tento postup přirozeně eliminuje výsledky neodpovídající standardnímu očekávání. Teorie komplexních systémů i praktická zkušenost však zahrnuje paradoxní jevy (projevem globálního oteplení může být extrémně mrazivá zima), které by nás měly určitě zajímat víc, než to, co stejně očekáváme.
• Druhým důvodem úspěšné existence může být stochastická povaha modelů, kterou jsme záměrně eliminovali. To nám umožnilo ověřit podstatu modelů. Pokud se však uvažují vozidla s náhodnými vlastnostmi, nedochází k synchronizaci chování vozidel a k možnému zesilování jejich reakcí.

Zjištěné problematické vlastnosti používaných modelů nejsou důvodem pro jejich zavrhnutí. Spíše by to mělo vést ke změně přístupu k výsledkům modelování a jejich interpretaci. Důvěřivé přijímání zjevené pravdy z černé skříňky, do které nasypeme nějaká data, nemálo peněz a stiskneme Enter není asi to pravé. Když se však rozhoduje o miliardových investicích na dopravní projekty, které ovlivní území na desítky, možná stovky let, výsledky modelování se používají jako tvrdý argument.

Vylepšování modelů je nezbytné, ale ani ono nikdy nepovede ke spolehlivě správným výsledkům. S dostupnými výsledky musíme nakládat podobně, jako jsme se to už naučili s předpověďmi počasí. Nic lepšího nemáme, ale nevěříme jim úplně. A známe u nich pravděpodobnost správné předpovědi v závislosti na délce předpovědi. Dopravní stavby se plánují na dvacet až třicet let, doba platnosti používaných modelů ověřená není. Doprava je závislá především na ekonomice, a ta sama o sobě je jen stěží predikovatelná (stačí si porovnat vývoj odhadů ekonomického vývoje v České republice zveřejňovaný od poloviny roku 2008). Anebo hledat úspěšného proroka, který by v roce 2008 předpověděl pětinový propad nákladní dopravy na zpoplatněných dálnicích.

ZÁVĚRY
Uvedené psycho-fyziologické modely jsou základem komerčně využívaných softwarových balíků (PTV VISSIM, Paramics), které se používají pro ověřování makroskopických charakteristik. Nerealistická simulace na mikroskopické úrovni jednotlivého vozidla patrně nepoškozuje zásadně požadované výsledky – především intenzity dopravních proudů. Pro podrobné zkoumání jevů na úrovni jednotlivého vozidla však tyto psycho-fyziologické modely nejsou vhodné, především pro nespojité chování a z toho plynoucí nestabilitu. K tomu přistupuje i nepřehlednost a komplikovanost použitých algoritmů, které jsou přes původní úmysl a navzdory pojmenování této kategorie modelů na hony vzdáleny reálnému chování vozidel.

Moderní přístupy kopírují metody používané v přírodních vědách: mikroskopický model by měl co nejvěrněji odrážet vlastnosti vozidla (resp. jeho řidiče). Při velkém výpočetním výkonu dnešních počítačů lze na základě takového modelu simulovat hromadné chování a sledované typické jevy (např. rychlost hustotních vln, jejich vzájemnou interakci apod.) ověřovat na reálném dopravním proudu. Při nesouladu je třeba zejména hledat jeho příčiny (malá výstižnost mikroskopického modelu), nikoli kalibrovat mikroskopický model tak, aby si patřičné statistické výsledky odpovídaly.

Mgr. Tomáš Apeltauer
Absolvoval Přírodovědeckou fakultu Masarykovy univerzity v Brně, obor Teoretická fyzika a astrofyzika. Nyní je asistentem na Ústavu informatiky Vysokého učení technického v Brně. Zabývá se hlavně modelováním dynamických systémů a objektově orientovaným programováním.

Ing. Petr Holcner, Ph.D.
Je absolventem Fakulty stavební VUT v Brně, oboru Konstrukce a dopravní stavby. V současnosti zde působí jako odborný asistent na Ústavu pozemních komunikací. Věnuje se projektování pozemních komunikací a dopravnímu inženýrstvím s důrazem na kritickou analýzu a modelování environmentálních dopadů dopravních řešení na společnost.

doc. RNDr. Jiří Macur, CSc.
Vystudoval Přírodovědeckou fakultu Masarykovy univerzity v Brně, obor Fyzika pevné fáze. V současné době je docentem na Ústavu informatiky Vysokého učení technického v Brně. Zabývá se zejména alternativními pohony, nelineární dynamickými systémy, jejich modelováním a využitím v inženýrských aplikacích.

LITERATURA:
[1] Apeltauer, T.; Holcner, P.; Macur, J.: Monitorování dopravního proudu – proč a jak?, článek v Silnice Železnice, ISSN 1801-822X, KONSTRUKCE Media, Ostrava, 2008
[2] Wiedemann, R.: Simulation des Strassenverkehrsflusses, Universität Karlsruhe, 1974
[3] Fritzsche, H. T.: A model for traffic simulation, Transportation Engininering, Contribution 5: 317–321, 1994
[4] Brockfeld, E., Wagner, P.: Calibration and Validation of Microscopic Traffic Flow Models, Traffic and Granular Flow 03, ISBN 3-540-25814-0 Springer-Verlag Berlin Heidelberg, 2005
[5] Olstam, J. J., Tapani, A.: Comparison of car-following models, LiTHITN-R-2004-5, Department of Science and Technology (ITN), 2004
[6] Macur, J.; Holcner, P.; Apeltauer, T.; Kyselý, M.: Modely dopravního proudu, článek v Silniční obzor, ISSN 0322-7154, 2005

RECENZE
Matematické modelování dopravních problémů je jedním z frekventovaných vědeckých témat. Přitom se ale akcent většiny odborných studií postupně posouvá od studia makroskopických dopravních fenoménů ke studiu dopravního mikrosvěta, tj. vzájemných interakcí mezi jednotlivými vozidly. Článek autorů T. Apeltauera, P. Holcnera a J. Macura se zabývá jedním z takových témat, konkrétně studiem akceleračních diagramů pro reálné dopravní vzorky a také pro provoz simulovaný prostřednictvím modelu inteligentního řidiče (tzv. IDM model). Taková srovnání modelu a dopravní reality jsou přitom velice důležitá při optimalizaci stávajících dopravních simulátorů. Prezentované výsledky proto shledávám velice přínosnými pro fyziku transportních systémů.

Mgr. Milan Krbálek, Ph.D., Katedra matematiky, Fakulta jaderná a fyzikálně inženýrská, ČVUT v Praze

Verification of some models of traffic flow
The development of transport modelling is not a closed topic even though the existence of commercially used modelling and simulation tools (software packages PTV VISSIM, Paramics) makes impression that the problem is solved and it is enough only to collect the right data. On the other hand, modern approach copies the methods used in natural sciences: microscopic model should truly reflect the features of the vehicle (or its driver). On the basis of such model, mass behaviour may be successfully simulated and the monitored typical phenomena (e.g. speed of density waves, their mutual interaction, etc.) may be verified on real traffic flow. During discrepancies, its causes have to be looked for (small accuracy of microscopic model), not to calibrate the microscopic model so that the relevant statistic results correspond.

Autoři

• Doc. RNDr. Macur Jiří Csc.
• Ing. Holcner Petr Ph.D
• doc. Mgr. Apeltauer Tomáš Ph.D.