Porovnání modelů pro výpočet hustoty dopravního toku
Rubrika: Zajímavosti
Tento příspěvek navazuje na předchozí práci publikovanou v tomto časopise v čísle 2/2013. Stejně jako v předchozím díle je i zde předmětem zkoumání srovnání přístupů k modelování dynamických dopravních jevů. Opět budeme pracovat s tzv. makromodelem pohlížejícím na modelovaný systém z globálního hlediska a mikromodelem, který vychází z chování základních stavebních elementů účastnících se děje. Tentokrát se zaměříme na analýzu výsledků získaných simulační technikou a řešením příslušné parciální diferenciální rovnice numerickou metodou. Zkoumány budou průběhy hustot vozidel v čase a prostoru. Cílem článku je opět porovnání výstupů obou modelů s důrazem na zachycení detailů přechodového jevu.
ÚVOD
Tato práce si klade za cíl porovnat výsledky dvou zcela rozdílných přístupů k modelování dynamiky dopravního proudu a navazuje na předchozí článek [6] publikovaný v tomto časopise. I zde ukážeme možné přístupy k modelování dopravních systémů, jejichž hlavním rozdílem je způsob pohledu na řešený problém.
Rozeznáváme tři základní skupiny modelů. První skupinu zastupují makromodely zaměřující se na celkové chování systému a vyžadující globální vstupní data. Opakem jsou pak mikromodely specializující se na detailní popis chování jednotlivých základních elementů modelu. My využijeme tzv. multiagentní přístup, kdy se model skládá z velkého množství objektů s autonomním chováním, které právě tímto chováním a uplatněním svých vzájemných vazeb vytvářejí globální charakteristiku celku. Mezi těmito dvěma přístupy pak můžeme najít ještě třetí; skupinu tzv. mezoskopických modelů, které kombinují prvky jak makromodelů, tak mikromodelů.
Náš příspěvek je strukturován následovně. Nejprve se zaměříme na matematické modelování vybraného přechodového jevu na základě podobnosti s proudem tekutiny v potrubí, které se řadí do kategorie makromodelů. Model je charakterizován hustotou, tokem a rychlostí dopravního proudu a lze jej popsat pomocí parciálních diferenciálních rovnic 1. řádu hyperbolického typu. Následuje stručné představení modelu a popis Laxovy-Friedrichsovy numerické metody, kterou jsme použili k řešení rovnice pro určení hustoty dopravního toku v daném čase a místě. Další kapitola přináší popis tvorby mikromodelu na základě multiagentního přístupu. Následuje popis počátečních podmínek, které byly zvoleny stejné jako v předchozím příspěvku. Závěrem uvádíme shrnutí výsledků experimentů s modely a jejich analýzu. Cílem je opět získat představu o vlastnostech jednotlivých modelů a potvrdit naše výzkumné očekávání shody výsledků obou experimentů a analyzovatklady a zápory použitých modelů.
MAKROSKOPICKÝ MODEL
Hustota a tok aut
Sledujme v daném časovém intervalu úsek silnice, kde rychlost dopravního toku je dána hodnotou funkce v(x,t) a hustota q je určena hodnotou funkce q(x, t) v místě x a čase t, kde t ≥ 0, x є R. Hustotu vozidel definujeme jako počet vozidel na jednotkovou délku silnice. Předpokládejme, že na daném úseku je dána maximální rychlost, označme ji vmax. Pak lze vyjádřit závislost rychlosti na hustotě následovně [3]: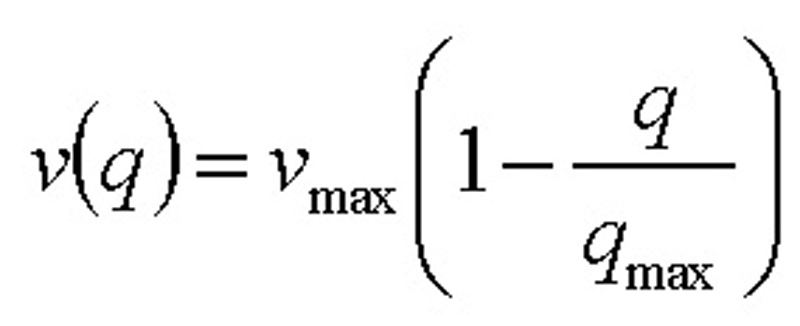 (1)
(1)
kde qmax je hustota, při níž dochází k zácpě a q ≤ qmax.
Tok vozidel představující počet vozidel, která projedou místem x za danou časovou jednotku t, budeme značit symbolem φ(x, t). Tokovou funkci vozidel budeme volit jako součin hustoty vozidel a rychlosti, jíž se vozidla pohybují, tedy následovně [3]: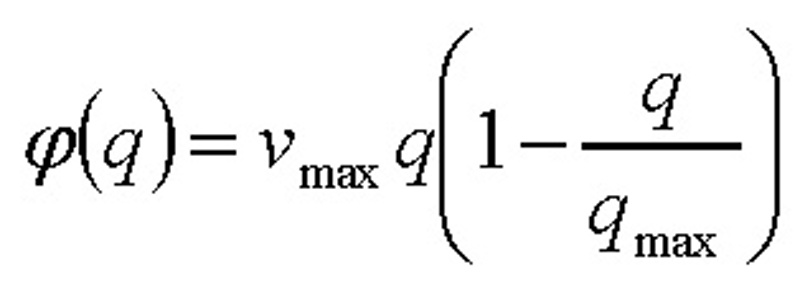 (2)
(2)
Odvození modelu
Pohyb vozidel na silnici lze popsat analogicky jako proudění tekutiny, jedná se tedy o zákon zachování počtu vozidel, tj. počet vozidel, který do daného úseku vjede, je totožný s počtem vozidel, která tento úsek opustí ve stejném časovém intervalu. Tuto závislost lze přepsat do podoby parciální diferenciální rovnice 1. řádu hyperbolického typu ve tvaru:![]() (3)
(3)
kde symbolem qt resp. φx značíme 1. parciální derivaci funkce q(x,t) podle proměnné t resp. 1. parciální derivaci funkce φ(x,t) podle proměnné x. Rovnici (3) dále můžeme přepsat do tvaru:![]() (4)
(4)
kde qx je 1. parciální derivace funkce q(x,t) podle proměnné x.
Rozložení hustoty vozidel v určitém čase a místě budeme moci určit, jakmile budeme znát rozložení hustoty vozidel v daném místě a čase. Nejčastější volbou podmínek je počáteční rozložení hustoty vozidel ve tvaru počáteční podmínky:![]() (5)
(5)
kde funkce q0(x) popisuje funkci q(x, t) v čase t = 0.
NUMERICKÉ METODY
Rovnici (4) s počáteční podmínkou (5) lze řešit analytickým způsobem např. metodou charakteristik nebo pomocí numerických metod. Oblast, která se zabývá numerickým řešením parciálních diferenciálních rovnic 1. řádu hyperbolického typu, je velmi rozsáhlá. Uvedeme zde stručný popis vybrané metody, kterou jsme použili pro numerické řešení naší konkrétní modelové situace. Jedná se o Laxovu-Friedrichsovu metodu, která se řadí do kategorie diferenčních metod. Diferenční metody jsou založeny na tom, že k aproximacím derivací využívají diferencí, v případě Laxovy- Friedrichsovy metody se jedná o diference centrální [4].
Popis metody
Interval, na kterém hledáme řešení, rozdělíme na daný počet N podintervalů, zde předpokládejme, že všechny podintervaly mají totožné délky. Označme (j+1)–ní bod dělení symbolem xj, j = 0,...,N a vzdálenost mezi sousedními uzly symbolem Δx, tedy platí xj = jΔx. Obdobným způsobem zavedeme konstantní dělení časového intervalu s časovým krokem Δt = tn+1 - tn, pro n ≥ 0 a platí tn = nΔt. Budeme předpokládat, že hodnota Δt/Δx je konstantní. Aproximaci přesného řešení v bodě xj a v čase tn označenou symbolem qnj budeme zapisovat jako Qnj. Diferenční formule lze odvodit např. pomocí Taylorova rozvoje. Pokud uvažujeme trojici sousedních bodů xj-1, xj a xj+1 a uzlové hodnoty vyjádříme Taylorovým rozvojem kolem prostředního bodu, pak lze metodu pro řešení nelineární úlohy (4) definovat následovně [4]: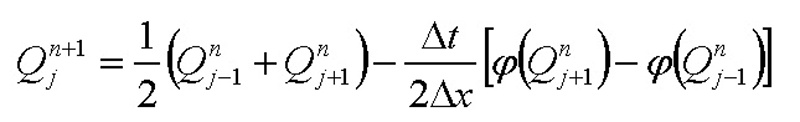 (6)
(6)
Tato metoda je známa pod názvem Laxova-Fridrichsova. Zvolíme-li tokovou funkci ve tvaru (2), pak vztah (6) přechází do podoby:
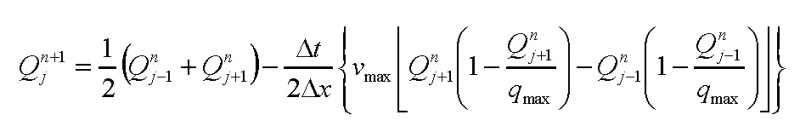 (7)
(7)
Podmínky konvergence metody
Úspěšnost použití popsané metody zaručuje tzv. Laxova věta, která tvrdí, že každá konzistentní lineární metoda je konvergentní právě tehdy, když je stabilní [5]. Stabilita metody zaručuje, že chyby, které můžou provázet vstupní data úlohy, jsou během výpočtu omezené. Stabilita může být důsledkem splnění tzv. Courantovy‑Friedrichsovy‑Lewyho (CFL) podmínky a to je tehdy, když platí vΔt/ Δx ≤ 1, v případě nelineární úlohy má CFL podmínka tvar:
max | φ´ (Qnj) | Δt / Δx ≤ 1.
Tato podmínka je v našem algoritmu testem kontrolována. Konzistence metody s danou diferenciální rovnicí představuje vlastnost, kdy příslušné diferenční schéma je v případě Δt → 0 totožné s danou diferenciální rovnicí. Pojem konvergence přibližného řešení k přesnému řešení pro Δt → 0 a pro Δx → 0 znamená tu vlastnost, že získané řešení lze libovolně zpřesňovat tím, že zmenšujeme velikost časového kroku. V tomto příspěvku se nebudeme dále tomuto tématu podrobněji věnovat.
SIMULAČNÍ MODEL
Popis modelu
V multiagentním modelu je chování celého systému modelováno jako agregace chování jednotlivých vozidel [2]. Globálními parametry jsou v tomto případě povolená rychlost v jednotlivých úsecích komunikace a frekvence výskytu vozidel, která byla nastavena na pevnou hodnotu 1 vozidlo za 3 s. Dalším globálním parametrem je pak délka vozidla stanovená na 4,5 m a minimální vzdálenost od vozidla bezprostředně před vozidlem zkoumaným stanovená na 0,5 m. Výše uvedená frekvence výskytu vozidel tak odpovídá hustotě 24 vozidel/km při maximální rychlosti 50 km/h.
Konceptuální model úlohy vychází z modelování vozidla jako samostatného agenta a jeho umístění do prostředí sledovaného úseku komunikace. Agent si také při své inicializaci ukládá informaci o agentovi bezprostředně před ním, aby jej mohl kontaktovat při zjišťování vzájemné vzdálenosti mezi vozidly.
Hlavní činností agenta během simulace je pohyb po sledovaném úseku komunikace, přičemž v pravidelných intervalech si agent kontroluje svou vzdálenost od vozidla před ním a na základě této vzdálenosti provádí úpravu své rychlosti tak, aby byla bezpečná (vzdálenost od předchozího vozidla bude při dané rychlosti minimálně 2 s). K implementaci modelu a znázornění výsledků byl využit softwarový nástroj AnyLogic [1].
PROVEDENÉ EXPERIMENTY
Počáteční podmínky
Sledovaný úsek komunikace o délce 1 000 m je rozdělen na tři části:
- 0 – 500 m s maximální rychlostí 50 km/h,
- úsek 500 – 600 m s maximální hustotou vozidel simulující kolonu před semaforem (maximální rychlost 0 km/h),
- úsek 600 – 1 000 m s maximální rychlostí 30 km/h.
Počáteční podmínka je zadána v 1. úseku hodnotou q1 = 24 vozidel/km, ve 2. úseku q2 = 200 vozidel/km (dopravní zácpa – qmax) a v posledním úseku je počáteční hodnota hustoty dána hodnotou 46 vozidel/km. V čase t = 0 s se na semaforu rozsvítí zelená barva a vozidla se začnou rozjíždět.
Grafické výsledky
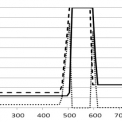
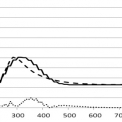
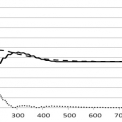
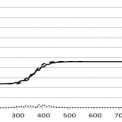
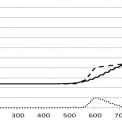
Řešený přechodový děj je možné pozorovat v rovině x - q, tedy sledováním hodnot hustoty vozidel v prostoru a konkrétním čase. Ilustrativní průběhy této hustoty podél celého sledovaného úseku v konkrétních časových okamžicích jsou znázorněny na obrázcích 1. až 5. První odpovídá času t = 0 s, kdy se v podstatě jedná o zobrazení vstupní podmínky a naskakuje zelená na semaforu. Následuje čas t = 120 s, kdy přechodový jev již probíhá. Další snímek hustoty byl pořízen pro čas t = 200 s, kdy přechodový jev vrcholí. Následuje snímek pro t = 326 s, kdy jev již začíná ustupovat a poslední snímek představuje situaci pro čas t = 432 s, kdy přechodový jev již odezněl. V obrázcích je rovněž vynesena křivka absolutních hodnot diferencí mezi hodnotami zjištěnými makromodelem a simulací.
Porovnání výsledků
Hlavním cílem našeho příspěvku bylo porovnání dvou metod popisu dynamiky dopravního toku za daných počátečních podmínek. Z prezentovaných grafů je patrné, že výstupy obou modelů jsou velmi podobné. Podkladem pro tento závěr je porovnání absolutních odchylek hodnot u obou modelů hustoty vynesené do grafů. Uvedená konstatování lze rovněž doložit hodnotami součtu absolutních hodnot odchylek hustoty vozidel u obou modelů pro konkrétní okamžikymodelového času. Z údajů plyne, že největší rozdíly byly na začátku přechodového děje, což je dáno především použitou metodou výpočtu hustoty vozidel v mikromodelu, která je zjišťována ze vzájemné vzdálenosti vozidel, takže jejich aktuální poloha velmi ovlivňuje celkový výsledek.
Hodnoty absolutních odchylek hustot q
| čas [s] |
Součet absolutních hodnot odchylek hustoty vozidel u obou modelů |
| 0 | 907,92 |
| 120 | 264,74 |
| 200 | 194,58 |
| 326 | 37,66 |
| 432 | 93,37 |
Je tedy možné formulovat závěr, že oba modely popsaly zvolený přechodový děj minimálně se lišícími kvantitativními hodnotami, čímž byla potvrzena hlavní hypotéza, kterou měl náš příspěvek ověřit. Numerický makroskopický model nemá možnost zachytit přechodový jev v takové míře detailu a je zde nutné řešit problém nespojitostí počáteční podmínky. Pro detailní zkoumání přechodového jevu je vhodnější model mikroskopický (simulační), který je však výpočetně náročnější a více ovlivnitelný lokálními situacemi v modelu. Po vytvoření modelu je však možné jej využít s relativně malými obměnami pro simulaci i jiných stavů systému.
ZÁVĚR
V našem příspěvku jsme se porovnali dva způsoby modelování hustoty vozidel v průběhu zvolené dopravní situace. Porovnávány byly simulační multiagentní model a matematický numerický model řešící parciální diferenciální rovnici hyperbolického typu. Výstupy obou modelů byly analyzovány s pomocí výpočtu absolutních hodnot odchylek obou modelů v čase, přičemž získané výsledky prokázaly, že modely jsou ve svých výstupech porovnatelné.
Naším záměrem je pokračovat v započatém výzkumu jeho zacílením na další dopravní situace a jevy. Analyzováno by také mohlo být širší spektrum zejména numerických modelů. Při užití mikroskopického přístupu je potřeba se zaměřit na věrnější modelování chování řidičů.
Článek byl vytvořen s podporou interního grantu č. 3/2013 při Vysoké škole technické a ekonomické v Českých Budějovicích.
Recenzovala:
doc. Ing. Bibiána Buková, Ph.D.
REFERENCE:
[1] AnyLogic Company, 1992-2012. AnyLogic. [Online] Available at: http://www.anylogic.com [Accessed 2. 11. 2012].
[2] Siebers, P. O. & Aickelin, U., 2008. Introduction to Multi-Agent Simulation. In: F. Adam & P. Humphreys, eds. Encyclopedia of Decision Making and Decision Support Technologies. Pennsylvania: Idea Group Publishing, pp. 554 – 564.
[3] LeVeque, R., J.: Finite Volume Methods for Hyperbolic Problems, Cambridge University Press 2002, pp. 203-213. ISBN 0521009243
[4] LeVeque, R., J.: Numerical Methods for Conservation Laws, Birkhauser Verlag,1990, Basel, ISBN: 3-7643-2464-3
[5] Míka, S., Přikryl, P.: Numerické metody řešení parciálních diferenciálních rovnic, Západočeská univerzita Plzeň, 1995, ISBN 80-7082-204-X
[6] Jelínek, J.,Vysoká J.: Modelování dynamiky dopravního proudu, Silnice železnice, 2/2013, 3-76 s., Konstrukce media, ISSN 1801-822X
Comparison of Models for Calculating the Density of the Traffic Flow
This paper follows previous work published in this journal issue 2/2013. As in previous work, two approaches for modeling dynamic traffic phenomena are examined. Again, we will work with the macromodel which looks at the modeled system from a global perspective and micromodel, which is based on the behavior of basic structural elements involved in the action. This time we focus on the analysis of the results obtained by multiagent simulation technique and the numerical solution of partial differential equations. The densities of vehicles in time and space will be examined. In the article we compare the outputs of both models with an emphasis on capturing the details of the transient phenomenon.