Zajímavosti
Zajímavosti  Jak parametry vjezdu okružní křižovatky ovlivňují bezpečnost silničního provozu
Jak parametry vjezdu okružní křižovatky ovlivňují bezpečnost silničního provozuJak parametry vjezdu okružní křižovatky ovlivňují bezpečnost silničního provozu
Rubrika: Zajímavosti
Nová výstavba nebo přestavba stávající křižovatky na okružní je běžnou praxí rozvoje a údržby silniční infrastruktury. Proto je vhodné znát vliv jejich parametrů na jízdu vozidla z pohledu bezpečnosti. Tento článek je zaměřen na analýzu přímého průjezdu vozidla okružní křižovatkou a s ním spojené charakteristiky. Měření probíhalo pomocí GPS jednotky umístěné v měřícím vozidle. Realizovali jsme cca 150 přímých průjezdů na 11 okružních křižovatkách v Brně. Identifikovali jsme parametry směrového polygonu jízdy vozidla: přímkovou a obloukovou část průjezdu a hodnoty úhlu na vjezdu, úhlu na přímém průjezdu, úhlu na výjezdu, poloměru vjezdu, průjezdu a výjezdu. Hlavním přínosem práce je stanovení vztahu mezi rychlostí vozidla na průjezdu a geometrií okružní křižovatky z pohledu bezpečnosti, které je vyjádřena dopravní nehodovostí. Výsledky potvrdily ovlivnění rychlosti vozidla vjezdovým poloměrem a úhlem. Závěry potvrzují nutnost dodržování vhodných návrhových parametrů křižovatky, abychom zaručili její bezpečnost, ale nenarušili propustnost.
ÚVOD
Okružní křižovatky (OK) představují jeden z nejdynamičtěji rozšiřujících se typů křižovatek na silniční infrastruktuře v ČR. Tento typ křižovatky se realizuje jako novostavba, ale častěji jako přestavba stávající stykové nebo průsečné křižovatky. Na území ČR jsme identifikovali cca 1 200 OK. Ke stavbě OK se přistupuje především z pohledu propustnosti a čím dál častěji i z pohledu bezpečnosti. Bezpečnost vychází z geometrického uspořádání křižovatky, které má přímý vliv na dráhu (trajektorii) projíždějících vozidel. Kapacita je geometrií OK také ovlivněna, především z pohledu rychlosti vozidel a plynulosti dopravního proudu.
Bezpečnost i kapacita křižovatky vychází nejen z jednotlivých průjezdů vozidel ale především z jejich interakce. Z pohledu ovlivnění okolním provozem lze rozlišit dva základní typy průjezdů a to: neovlivněný (bez interakce) a ovlivněný průjezd (s interakcí). Na oba typy má vliv geometrie a uspořádání křižovatky (komunikace), které zůstávají neměnné. Od těchto faktorů se odvíjí reakce řidiče a dále pak pohyb vozidla. Jejich vliv na bezpečnost lze identifkovat pomocí multifaktorové analýzy ve vztahu k parametrům neovlivněných průjezdů.
Uspořádání OK nedovoluje levé odbočení. Sdružuje pohyb vozidel jednoho paprsku křižovatky do jednoho vjezdu (směru), kde řidiči dávají přednost vozidlům na okruhu. Vjezd je nejčastějším místem konfliktů a dopravních nehod v oblasti OK. Jeho úprava ovlivňuje rychlost a trajektorii vozidla na průjezdu křižovatkou.
Na území ČR se nachází poměrně široká škála realizovaných vjezdů OK, které umožňují jak nízké tak vysoké rychlosti vozidel. O rychlosti je známo, že má přímý vliv na brzdnou dráhu vozidla (bezpečnost) ale i propustnost křižovatky (kapacita). Článek je specificky zaměřen na analýzu trajektorie přímého průjezdu OK. Základním předpokladem je, že vhodnou realizací vjezdu a středového ostrova křižovatky jsou řidiči motivováni upravit rychlost vozidla, což má vliv na vznik a průběh konfliktů či dopravních nehod.
SMĚROVÝ POLYGON NA PŘÍMÉM PRŮJEZDU OKRUŽNÍ KŘIŽOVATKOU
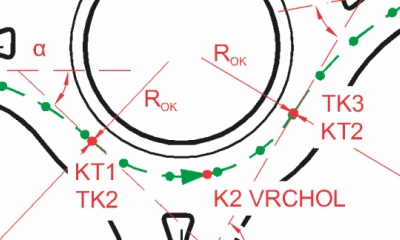
Přímý průjezd je v této práci definován jako pohyb vozidla mezi dvěma protilehlými rameny OK (z vjezdu do protilehlého výjezdu). Trajektorie představuje pohyb vozidla zaznamenaný GPS (zelené body na obr. 1).
Tato práce uvažuje, že trajektorii vozidla na průjezdu křižovatkou lze rozložit a zjednodušit pomocí prvků směrového polygonu (přímky a směrové oblouky viz obr. 1). Trajektorie obsahuje přímku na vjezdu, pravý směrový oblouk na vjezdu, levý směrový oblouk na okruhu křižovatky, pravý směrový oblouk na výjezdu křižovatky a přímku za výjezdem. Mezi přilehlými oblouky uvažujeme inflexní bod (bod TK = KT). Naměřenou krátkou (L < 1 m) mezi přímou zanedbáváme. Tečny tvoří směrový polygon. Přímky polygonu spolu svírají úhly (postupně ve směru jízdy α, ω, β). Na obr. 1 jsou prezentovány ostrůvky o minimálních parametrech.
Úhel na vjezdu OK (α viz obr. 1) představuje změnu směru jízdy vozidla při vjezdu na okružní pás. Úhel na přímém průjezdu křižovatkou (ω viz obr. 1) představuje změnu směru pohybu vozidla při objíždění středového ostrova. Úhel na výjezdu OK (β viz obr. 1) představuje změnu směru jízdy vozidla při výjezdu z okružního pásu.
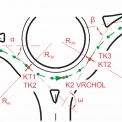
U nevhodně navržených OK nabývají úhly α, ω nebo β hodnot blížících se nule. Vozidlo pak projíždí téměř nebo úplně po přímce (viz oranžové nebo červená čára na obr. 2). Následkem toho nedochází k redukci rychlosti. Na obr. 2 je zobrazen vliv zmenšujícího se poloměru středního ostrova na úhel na přímém průjezdu ω. Rychlost vozidla na průjezdu obloukem by se měla pohybovat maximálně mezi 30 – 35 km/h (dle TP 135 [2]), jinak dochází ke zvýšení počtu DN nebo závažnějším následkům.
Do směrového polygonu jsou vloženy směrové oblouky, které nahrazují reálnou křivku průjezdu. Oblouk náleží vždy mezi dvě tečny (přímky), které svírají příslušný směrový úhel (α, ω, β). Návrhovými poloměry na vjezdu/průjezdu/výjezdu OK se zabývá např. publikace Traffic and Highway Engineering [9], která je odvozuje dle obalových křížovek jednotlivých typů vozidel s ohledem na jejich rychlost. V ČSN 73 6102 [1] je uvedena maximální hodnota poloměru R < 100 m na přímém průjezdu OK. Nově revidované TP 135 [2] doporučují korigovat průjezd vozidla pomocí pojížděného prstence (podrobněji viz diskuze).
DATA
Výběrový soubor zahrnoval 155 průjezdů měřícího vozidla na 11 OK ve městě Brně (v intravilánu). Jedno měření představovalo neovlivněný přímý průjezd měřícího vozidla křižovatkou z vjezdu do protilehlého výjezdu. Průjezdy byly realizovány v běžný pracovní den měsíce října 2016 (v ranních a nočních hodinách mimo špičkové zatížení). Cílem bylo získat měření z průjezdů, které byly realizovány bez ovlivnění jinou dopravou. Z původního vzorku byly odstraněny ty průjezdy měřícího vozidla, u kterých byla zaznamenána interakce s jinými účastníky silničního provozu. Počet průjezdu byl redukován na 92 platných průjezdů (viz následující tab. 1).
Tabulka 1 – Analyzované křižovatky: Brno
| Okružní křižovatka | Počet ramen |
Trajektorie |
Průměrná hodnota [m] |
Průměr OK |
Průměrná hodnota [̊°] |
||||
| RIN | ROK | ROUT | α | ω | β | ||||
| Dlouhá × Hraničky | 4 | 21/21 | 29 | 17 | 36 | 30 | 37 | 76 | 33 |
| Hlavní × Absolonova | 4 | 10/10 | 34 | 19 | 38 | 33 | 35 | 79 | 33 |
| Hudcova × Kytnerova | 3 | 10/6 | 25 | 19 | 30 | 30 | 34 | 54 | 45 |
| Hviezdoslavova × Bedřichovická | 4 | 18/9 | 56 | 24 | 52 | 27 | 15 | 46 | 16 |
| Jihlavská × Stará dálnice | 4 | 18/12 | 37 | 19 | 34 | 35 | 26 | 70 | 32 |
| Koperníkova × Lazaretní | 4 | 10/9 | 28 | 23 | 38 | 31 | 36 | 71 | 33 |
| Kšírova × Sokolova | 4 | 21/1 | 41 | 19 | 32 | 31 | 31 | 78 | 34 |
| Odbojářská × Nad Kašnou | 4 | 8/1 | > R* | 20 | 35 | 29 | 2 | 68 | 21 |
| Palachovo náměstí | 4 | 10/8 | 27 | 24 | 26 | 48 | 49 | 92 | 50 |
| Slezákova × Kohoutova | 3 | 12/6 | 24 | 19 | 64 | 32 | 64 | 75 | 15 |
| Vídeňská × FUTURUM | 4 | 9/9 | 33 | 20 | 26 | 35 | 33 | 76 | 40 |
| Poznámka: * Jedná se o vysokou hodnotu poloměru R, která se blížila nekonečnu (oblouk inklinuje přímce). | |||||||||
Měření probíhalo pomocí měřícího vozidla, které obsahuje zařízení pro měření fyzikálních veličin s přesnou lokalizací objektů v systému GPS (jednotka Mti 100-series, horizontální přesnost: 1 m) a videozáznam projížděné komunikace. Měření realizovali dva řidiči.
Tato práce představuje sběr a analýzu dat, která zanedbána rozmanitost vozového parku a řidičů. Průjezdová křivka vozidla byla nahrazena kružnicí. V budoucnosti se chce CDV věnovat další analýze tohoto typu křižovatky a doplnit chybějící údaje (výhledově v roce 2018).
METODA
Analýza trajektorie pohybu vozidla spočívá v rozboru skupiny po sobě jdoucích bodů, které definují polohu vozidla vůči počátku souřadnicového systému (původní GPS transformováno do S-JTSK). Trajektorie je vytvořena odečítáním charakteristik polohy měřícího vozidla za pohybu v reálném čase. Skutečná dráha vozidla byla nahrazena řadou bodů, které v pravidelných časových intervalech odečítala jednotka GPS. Pro rozbor je nejpodstatnější směrový úhel φ a odchylka směru Δφ po sobě jdoucích bodů trajektorie.
U oblouku je nezbytné identifikovat počáteční (TK), mezilehlý blízký prostřednímu (vrchol K) a koncový bod (KT). Řešením soustavy tří rovnic o třech neznámých (dosazením do obecné rovnice pro kružnici se středem v bodě) získáme polohu středu a hodnotu poloměru. Na základě polohy středu kružnice, počátku a konce oblouku se vypočte úhel na vjezdu α, který je dle konstrukce směrového polygonu (přímka, kružnice, přímka) stejný jak v jeho vrcholu, tak ve výseči oblouku. Stejným postupem se stanoví parametry pro všechny oblouky trajektorie vozidla. Na následujícím obr. 3 je prezentována identifikace prvků směrového polygonu trajektorie vozidla na přímém průjezdu OK. Směrové oblouky jsou identifikované na základě nenulových hodnot rozptylu a směrodatné odchylky směrového úhlu Δφi.
Následuje popis charakteristik průměrného směrového polygonu trajektorie na přímém průjezdu OK z reálného měření pomocí měřícího vozidla. Tyto charakteristiky byly odvozeny pomocí analýzy trajektorie vozidla.
Tabulka 2 – Charakteristiky směrových polygonů výběrového vzorku
| Charakteristika | Min. | Max. | Průměr |
Směrodatná odchylka |
Rozptyl | Jednotka |
| Úhel na vjezdu – Alfa | 2 | 83 | 35 | 17 | 281 | [̊°] |
|
Úhel na přímém průjezdu |
28 | 125 | 73 | 20 | 381 | [̊°] |
| Úhel na výjezdu – Beta | 3 | 63 | 32 | 14 | 190 | [̊°] |
| Poloměr na vjezdu RIN | 15 | > R* | 34 | 14** | 206** | [m] |
| Poloměr na průjezdu ROK | 12 | 49 | 20 | 5 | 26 | [m] |
| Poloměr na výjezdu ROUT | 18 | > R* | 37 | 18** | 328** | [m] |
|
Rychlost v bodě 50 m |
27 | 60 | 42 | 8 | 40 | [km/h] |
| Rychlost v bodě TK 1 | 15 | 40 | 31 | 6 | 32 | [km/h] |
| Rychlost v bodě KT 1 = KT 2 (KK) | 13 | 36 | 26 | 5 | 22 | [km/h] |
| Rychlost v bodě vrchol K2 | 11 | 34 | 24 | 5 | 22 | [km/h] |
| Rychlost v bodě KT 2 = KT 3 (KK) | 14 | 50 | 30 | 6 | 33 | [km/h] |
| Rychlost v bodě KT 3 | 23 | 52 | 38 | 7 | 45 | [km/h] |
|
Rychlost v bodě 50 m |
28 | 68 | 44 | 9 | 87 | [km/h] |
|
Poznámka: |
||||||
VZTAH RYCHLOSTI A GEOMETRIE OK
Pro posouzení vztahu rychlosti vozidla V, poloměru (RIN, ROK, ROUT) a úhlu (α, ω, β) průjezdu byl použit Spearmanův korelační koeficient. Korelace vyšší jak 0,5 byla zaznamenána pouze u následujících parametrů:
- rychlost vozidla V50m před vjezdem a úhel na vjezdu α,
- rychlost vozidla V50m před vjezdem a poloměr vjezdu RIN,
- rychlost vozidla ve vrcholu okružního pásu VK2vrchol a poloměr průjezdu na okruhu ROK.
Korelace vypovídá o vztahu mezi aktuální rychlostí vozidla na průjezdu V a prvky směrového polygonu (úhly, poloměry). Předpokladem je, že řidič volí rychlost vozidla dle parametrů komunikace, které předcházejí jeho trase. Na základě dat z měření lze potvrdit, že rychlost vozidla na přímém průjezdu OK koreluje s geometrií OK. Přitom korelace rychlosti V50m před vjezdem a poloměrů RIN je vyšší jak korelace s úhlem na vjezdu α. Obdobných výsledkům dosáhla i studie rychlostních charakteristik na přímém průjezdu OK [3].
Hodnota nejvyšší korelace byla zaznamenána mezi rychlostí vozidla před vjezdem na OK (V50m před vjezdem) a rychlostí ve všech ostatních bodech průjezdu. To značí, že se chování řidiče v průběhu průjezdu OK nemění, jelikož nekoreluje s jinými parametry. Pokud řidič vjíždí „vysokou“ rychlostí do OK, tak průjezd a výjezd z OK provádí také vysokou rychlostí.
V místě napojení na okruh křižovatky (KT1 = TK2) má stále největší vliv jeho vjezdová rychlost V50m před vjezdem a až potom poloměr okruhu ROK a úhel na přímém průjezdu ω, což jsou směrové prvky komunikace, která předchází jízdě vozidla.
V místě vrcholu K2 je obvykle pro řidiče již viditelný výjezd OK. I tak byla zaznamenána vyšší korelace s původní vjezdovou rychlostí vozidla (V50 m před) než poloměru ROUT a úhlu na výjezdu β. V bodech trajektorie za výjezdem se řidič snaží vrátit ke své původní (vjezdové) rychlosti vozidla V a reaguje na další situaci mimo oblast OK.
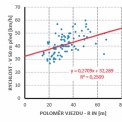
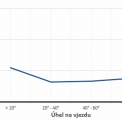
Na grafech (obr. 4 a obr. 5) je prezentován průběh závislosti rychlosti měřícího vozidla V50 m před na úhlu na vjezdu α a poloměru vjezdu RIN. Vyšší hodnoty úhlu na vjezdu α vedou k nižším rychlostem (viz obr. 4). Vyšší hodnoty poloměru vjezdu RIN vedou k vyšším rychlostem (viz a obr. 5). Pro snížení rychlosti je logické vybírat vyšší hodnoty úhlu na vjezdu α a nižší hodnoty poloměru na vjezdu RIN. Přitom je nutné brát ohled na závislost poloměru RIN na úhlu vjezdu α (viz obr. 6). Nízké hodnoty úhlu na vjezdu α vedou k vysokým hodnotám poloměru, které se blíží přímce.
PRŮBĚH RYCHLOSTI VOZIDLA NA PŘÍMÉM PRŮJEZDU OK
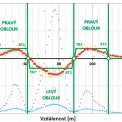
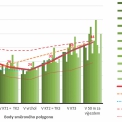
Na následujícím obr. 7 je zobrazen průběh průměrné měřené rychlosti V vozidla (červená čára) z 92 realizovaných průjezdů. Rychlost vozidla na průjezdu je nejnižší ve vrcholové části oblouku, který náleží okružnímu pásu křižovatky. Zelené sloupce udávají hodnoty průměrné rychlosti V z jednotlivých trajektorií průjezdu v rámci konkrétní křižovatky. Nutné je připomenout, že se jedná o neovlivněné průjezdy.
Vyšší hodnoty rychlostí V odpovídají nízkým hodnotám směrových úhlů (α, ω, β) a velkým hodnotám směrových oblouků (RIN, ROK, ROUT), což vede k přímému průjezdu křižovatkou (na obr. 7 znázorněno červenou čárkovanou čarou). Z pohledu bezpečnosti je toto nežádoucí.
Naopak nízké hodnoty rychlostí V odpovídají vysokým hodnotám směrových úhlů (α, ω, β) a malým hodnotám směrových oblouků (RIN, ROK, ROUT), což vede k vychýlení trajektorie vozidla na průjezdu křižovatkou (na obr. 7 znázorněno červenou tečkovanou čarou). Z pohledu bezpečnosti je toto výhodné. Z pohledu propustnosti dochází ke snížení kapacity křižovatky (tj. narušení plynulosti dopravního proudu).
Experimentálně je dále na obr. 7 zobrazen průběh, pro tuto práci nazvané kapacitní rychlosti V (oranžová čárkovaná čára). Ta vychází z předpokladu, že přibližující se vozidlo k OK má zpomalit v místě vjezdu (TK1), kde z pravidla dává přednost v jízdě vozidlům na okruhu. Toto splňuje požadavky na bezpečnost. Dále však nemá důvod, svoji rychlost snižovat, takže může svoji rychlost opět plynule zvyšovat až na původní hodnotu za výjezdem z OK. To za předpokladu, že se jedná o nekonfliktní průjezd. Jedná se tedy o velmi „kapacitní průjezd“ právě jednoho vozidla.
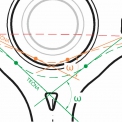
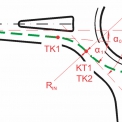
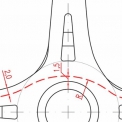
Dle revidovaného vydání TP 135 [2] je požadováno vychýlení trajektorie osobního automobilu na přímém průjezdu OK. Toto vychýlení má být zajištěno rozměry a umístěním středového ostrova a prstence spolu s ostatními prvky OK. Trajektorie pohybu vozidla se uvažuje dle obr. 8. Současně je zde popsán požadavek, že odchylka dráhy vozidla projíždějícího OK mezi dvěma protějšími nebo sousedními paprsky křižovatky nemá umožnit rychlost vyšší jak: 30 km/h na OK s jedním pruhem na okruhu, 50 km/h na OK se dvěma a více pruhy na okruhu (viz obr. 9).
Odchylka dráhy vozidla je popsána v kapitole 3.2.3. TP 135 [2] následovně: „V místě napojení paprsku křižovatky na okružní pás je doporučeno provést mírné vychýlení jízdních pruhů na vjezdu i výjezdu (5–15° směrem od osy paprsku). Tím se zajistí zpomalení vozidel přijíždějících k okružnímu pásu, usnadní průjezd rozměrných vozidel a oddálí se vjezdy od výjezdů. Tato úprava má pozitivní vliv na kapacitu křižovatky.“
Na obr. 8 je toto vychýlení označeno jako α0. Domníváme se, že vychýlení jízdního pruhu na vjezdu nedonutí řidiče ke snížení rychlosti. Takovou změnu směru jízdy vozidla v intravilánové rychlosti řidič nepocítí. Maximální měřená rychlost na průjezdu s vychýlením pomocí dlouhého ostrůvku je prezentována na obr. 7 (červená čárkovaná čára, OK Brno, Hudcova – Kytnerova). Hlavní prvek sloužící ke snížení rychlosti vozidla je úhel na vjezdu (α1), proto jsme zanedbali vliv vychýlení jízdního pruhu paprsku křižovatky α0.
Technicky se celkové vychýlení dráhy vozidla α skládá z vychýlení jízdního pruhu v patřičné vzdálenosti před napojením na okruh (viz obr. 8 označeno jako α0) a dále potom v místě napojení na okruh (viz obr. 8 označeno jako α1). Vychýlení v místě napojení na okruh se zpravidla provádí polohou středového ostrova, pojížděným prstencem, ale také poloměrem zakružení vjezdu.
Úprava tohoto charakteru má zajistit dostatečné vychýlení trajektorie vozidla bez zbytečného snížení rychlosti a vytvořit tak prostor pro ostrůvek a také větší vzdálenost kolizních bodů na okruhu křižovatky. To podpoří rozhledové pole a reakční dobu řidičů.
VLIV PRVKŮ OKRUŽNÍ KŘIŽOVATKY NA NEHODOVOST
Model nehodovosti vjezdu OK z pohledu trajektorie vozidla (viz vzorec (1)) identifikoval vliv intenzity I, úhlu na vjezdu α a přibližující se rychlosti vozidla V50 m před na vznik dopravní nehody. Model potvrdil, že:
- s rostoucí hodnotou intenzity I bude počet nehod N klesat,
- s rostoucí hodnotou úhlu na vjezdu α bude počet nehod N klesat,
- a že s rostoucí hodnotou přibližující rychlosti vozidel V50m před bude počet nehod N růst.
Model nehodovosti vjezdové části trajektorie![]()
- Závislost klesajícího počtu nehod N na rostoucí intenzitě I je neobvyklá. Lze ji však vysvětlit vyšším podílem malých mezer v intravilánu a vyšší intenzitou, která znamená menší rozestupy mezi vozidly, přirozeně nižší rychlost a větší pozornost řidičů.
SHRNUTÍ A ZÁVĚR
Z pohledu bezpečnosti vedou nízké hodnoty úhlu na vjezdu α k vyšší rychlosti vozidla V což je v místě vjezdu OK nebezpečné (způsobuje horší následky nebo vyšší počet nehod). Z výsledků korelace a multifaktorové analýzy vyplývá, že parametry trajektorie vozidla na přímém průjezdu OK jsou ovlivněny vjezdem křižovatky, a to následovně:
- s rostoucím poloměr vjezdu RIN roste přibližovací rychlost vozidla,
- vyšší hodnoty úhlu na vjezdu vyžadují menší hodnoty poloměru vjezdu RIN,
- větší úhel na vjezdu α snižuje pravděpodobnost vzniku nehody (viz obr. 10).
OK je tedy vhodné navrhovat s dostatečným směrovým vychýlením a poloměrem vjezdu. Požadavky na směrové vychýlení na vjezdu OK jsou popsány v současném znění TP 135 [2]. Uvedená hodnota vychýlení 5 až 15 ° však z pohledu bezpečnosti v intravilánu nepostačuje, jelikož nedochází k přínosné redukci rychlosti.
Z pohledu kapacity je nutné poznamenat, že úprava směru jízdy má vliv na rychlost vozidla na průjezdu a ovlivňuje tak plynulost dopravního proudu. V případě komunikace vyšší kategorie nebo nízkých intenzit toto není výhodou, ale časovou ztrátou.
Tento článek byl vytvořen za finanční podpory Ministerstva školství, mládeže a tělovýchovy v rámci programu Národní program udržitelnosti I, projektu Dopravní VaV centrum (LO1610) a na výzkumné infrastruktuře pořízené z Operačního programu Výzkum a vývoj pro inovace (CZ.1.05/2.1.00/03.0064).
Autoři: Ing. Jan Novák, Ph.D., Ing. Lucie Vyskočilová, Ing. Jiří Ambros, Ph.D., Centrum dopravního výzkumu, v. v. i.
RECENZE
Ing. Zuzana Čarská, Ph.D.,
ČVUT, Fakulta dopravní
Článek informuje o výsledcích analýzy přímého průjezdu okružní křižovatkou z hlediska dopadů konkrétních návrhových parametrů jednotlivé okružní křižovatky na bezpečnost silničního provozu. Průzkum provedli na dostatečně rozsáhlém souboru přímých průjezdů na přiměřeně pestré skladbě (z hlediska stavebního uspořádání resp. geometrie křižovatky) 11 okružních křižovatek. Velmi zajímavým a překvapivým závěrem z analýzy je zjištění, že nejvyšší korelace se objevila mezi rychlostí 50 m před vjezdem a rychlostí ve všech ostatních bodech průjezdu. Jinými slovy řečeno, chování řidiče se průběhu přímého průjezdu křižovatkou již tolik nemění v důsledku uspořádání křižovatky, ale pokud vjel rychle do ní, pak rychle projíždí i celou samotnou křižovatkou. Souhrnné závěry analýzy (dole na str. 7) jsou poměrně logické. Důležitým přínosem analýzy je mimo jiné také zjištění, že hodnota vychýlení na vjezdu 5° až 15°, doporučována v TP 135, není z pohledu bezpečnosti dostatečná.
(Formálně kompletní recenzi má redakce uloženou ve svém archivu.)
REFERENCE:
[1] ČSN 73 6102 Projektování křižovatek na silničních komunikacích, edice č. 2, červen 2012, Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, 2012
[2] TP 135 Projektování okružních křižovatek na silničních a místních komunikacích, Ministerstvo dopravy ČR, duben 2017
[3] Sangyoup K., Jaisung Ch., Safety Analysis of Roundabout Designs based on Geometric and Speed Characteristics, KSCE Journal of Civil Engineering (2013) 17(6):1446-1454, DOI 10.1007/s12205-013-0177-4
[4] Bared J. G., Prosser W., Esse C. T., State of the Art Design of Roundabouts, Transportation Research record 1579, No. 970969
[5] Design Guide on Inter-Urban Roundabouts (in French). SETRA, France, 1996.
[6] Beau B., Alsghan I., Li-Hong Chiu, Andrea R. Bill, and David A. Noyce, Analysis of Rear-End Collisions at Roundabout Approaches, Transportation Research Record: Journal of the Transportation Research Board, No. 2585, Transportation Research Board, Washington, D.C., 2016, pp. 29–38. DOI: 10.3141/2585-04
[7] Turner S. A., Roozengurg A. P., Smith A. W., Roundabout crash prediction models, June 2009, NZ Transport Agency research reposrt 386.
[8] Roundabouts – Application and design, A practical manual, Ministry of transport, Public Works and Water management, partners for Roads, June 2009, file: B5381-01.001, registration number: VB/SE2008.0772
[9] Nicholas J. Garber, Lester A. Hoel, Traffic and Highway Engineering 5th Edition, ISBN-13: 978-1133605157, ISBN-10: 113360515X
How Do Roundabout Entry Design Parameters Influence Safety
Roundabouts (either new-builts or conversions) present a common practise of road network development. I tis therefore important to know the influence of roundabout parametres on driving and safety.The paper focuses on analysis of roundabout through-pass. Measurement was done using GPS in an instrumented vehicle, in a total of 150 through-drives at 11 roundabouts in Brno. We identified trajectory parameters, including tangents, curves, entry angles, deviation angles and exit angles. The main contribution was in determining the influence of roundabout geometry on driving speed and safety. The conclusions confirm the necessity of suitable design parameters to ensure both safety and capacity.