Chování bezstykové koleje na mostě s velkým dilatačním zařízením

Při zřizování koleje na mostních objektech je všude tam, kde to dovolují podmínky, dávána přednost konstrukci bezstykové koleje (BK). Při zřizování BK na mostních objektech s otevřeným kolejovým ložem platí stejné zásady jako pro BK na zemním tělese. Na mostním objektu s ložisky jsou rozhodujícím faktorem dilatující délky nosné konstrukce. Bezstykovou kolej na mostních objektech s dilatujícími konstrukcemi s kolejovým ložem i bez kolejového lože lze zřídit podle předpisu SŽDC S3 Železniční svršek, Díl XII, jsou-li dilatující délky nosných konstrukcí menší nebo rovné největším přípustným dilatujícím délkám zde uvedeným. Pro mosty s nosnými konstrukcemi betonovými nebo ocelobetonovými a s pražci betonovými nebo dřevěnými jsou přípustné dilatační délky podle tvaru kolejnice 80 m až 180 m. V případě větších dilatačních délek je třeba provést samostatné řešení. Takové řešení se nachází např. na I. koridorové trati na mostním objektu Parník – Dlouhá Třebová, na estakádách tramvajové tratě Hlubočepy – Barrandov v Praze nebo na mostech Nového spojení trati Praha hl. n. – Libeň, resp. Vysočany. Na těchto mostech byla prováděna dlouhodobá měření v konstrukcích koleje a mostu, která ukázala reálné hodnoty vzájemného pohybu kolejnicových pásů BK a mostní konstrukce v závislosti na změně teploty ovzduší, resp. mostu.

Měření na Novém spojení na mostě přes Masarykovo nádraží probíhala v letech 2008 až 2012. Dilatující délka mostní konstrukce je v tomto případě 439 m. Na mostě je zřízena BK na betonových pražcích v kolejovém loži ve žlabu. Nosná konstrukce mostu je komůrkový betonový předpjatý spojitý nosník o 12 polích. Železniční svršek tvoří kolejnice UIC 60, pružné upevnění W14, betonové pražce B91S, rozdělení pražců v koleji „u“, kolejové lože na estakádě je ve žlabu. Tloušťka kolejového lože je min. 510 mm od úložné plochy pražce a to v celé šířce žlabu. Umístění mostních závěrů (MZ) estakády je v přechodnici oblouku 750 m bez převýšení (směr žst. Praha – Libeň), resp. v oblouku levostranném s poloměrem 578 m bez převýšení (směr žst. Praha – Vysočany), ve sklonu 3,3 ‰. Při dilatující délce mostní konstrukce L_T = 439 m bylo nutné použít ve všech kolejích na straně pohyblivého ložiska velmi velké kolejové dilatační zařízení (KVVDZ) v každé koleji. Zde bylo zvoleno dilatační zařízení DZ 60 – 1:40b s pohyblivou kolenovou kolejnicí. KVVDZ je umístěno tak, že pohyblivá kolenová kolejnice vychází z mostní konstrukce, pevná jazyková kolejnice je ze strany trati. Začátek jazykové kolejnice je cca na jedenáctém pražci od MZ.

Pro měření pohybu kolenové kolejnice v dilatačním zařízení byly zvoleny dvě metody, které dlouhodobě zaručovaly kontinuitu měřených dat při případném poškození měřící báze, tzn. po dobu pěti let (2008 až 2012). Měření byla realizována během jednotlivých ročních období v závislosti na klimatických podmínkách.

V prvním případě byla zvolena metoda měření vzájemné polohy kolenové a jazykové kolejnice pomocí ocelového měřítka na stojině kolenové kolejnice. Ve druhém případě je zvolena metoda, při které byly do hlavy kolejnicových pásů vyvrtány otvory pro odečet vzdálenosti na měřící bázi pomocí speciálního posuvného měřítka. Obě metody byly vyhodnocovány současně. Pro porovnání pohybu mostní konstrukce a dilatačního zařízení byly zabudovány do závěrné zídky, resp. mostní přepážky, fixní body představující další měřící bázi. Naměřené hodnoty všech posunů byly přepočteny k teplotě +10 °C, tedy shodné pro mostní konstrukci a kolejnici a tato teplota byla stanovena jako výchozí. Vzájemný pohyb pražců a mostní konstrukce byl sledován geodetickou metodou. Současně s měřením posunů ve KVVDZ a mostu byla registrována teplota ve spodní části mostní konstrukce (dále teplota mostu) v místech, která nebyla osvícena slunečními paprsky a okamžitá teplota kolejnicových pásů. Celkem bylo provedeno 20 souborů měření v rozsahu teploty kolejnicových pásů <–23;+40> °C.

VÝPOČET PODÉLNÉHO ODPORU PROTI POSUNUTÍ
Pomocí výše popsaného dlouhodobého sledování byl získán dostatečně velký soubor dat, který umožní stanovit skutečně působící měrný odpor proti podélnému posunutí kolejnice a mostní konstrukce a následně celkovou smykovou sílu v úrovni kolejnicového pásu v místě MZ. Řešení modelu konstrukce je popsáno na následujících řádcích.

Volba výpočetního modelu a rovnice popisující řešený problém
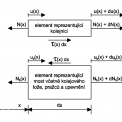
Jako základní výpočtový model byl zvolen 1D model sestávající ze dvou spolupůsobících elastických elementárních dílů, z nichž jeden představuje kolejnicový pás a druhý most včetně kolejového lože, pražců a upevnění. Vzájemné spolupůsobení obou dílů je v modelu reprezentováno zavedením podélných smykových sil τ [kN·m^–1], působících na styku obou částí modelu. Takový model byl zvolen v souladu s výsledky měření, které ukázaly, že ke vzájemnému pohybu pražců a mostní konstrukce nedochází. Celý model je zobrazen na obr. 1.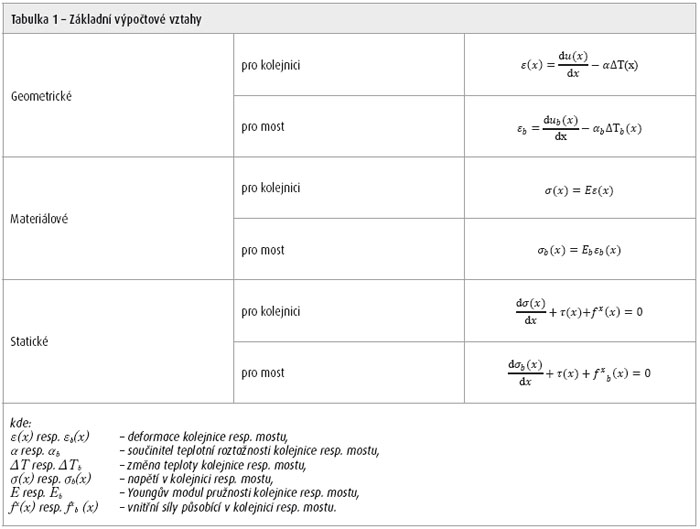

Osa x je orientována zleva doprava a v souladu s konvencí jsou zavedeny následující veličiny:

u(x) – posun kolejnice,
u_b(x) – posun mostu,
N(x) – normálová síla v kolejnici.
N_b(x) – normálová síla v mostu,
τ(x) – podélné smykové síly mezi mostem a kolejnicí – podélný odpor proti posunutí.

Za základní rovnice je považována obvyklá trojice geometrických, materiálových a statických rovnic, které platí vždy zvlášť pro jednotlivé části modelu. Z Tabulky 1 vyplývá, že materiál mostu je považován za homogenní, tedy veškeré materiálové charakteristiky jsou uvažovány po průřezu konstantní, a materiálové chování je pouze lineárně pružné dle Hookeova zákona (Tabulka 1). Celková deformace je prostým součtem deformace silové a teplotní.

Měření byla prováděna na mostě, který v okamžiku měření nebyl zatížen podélnými silami od provozu, je uvažováno f^x(x) = f^x_b (x) = 0. Taktéž změna teploty je uvažována jako rovnoměrná, tedy v daný časový okamžik po celém tělese prutu stejná (teplota tedy není funkcí souřadnice x).

Spojením všech tří druhů rovnic z Tabulky 1 vznikne soustava diferenciálních rovnic, popisujících daný problém:

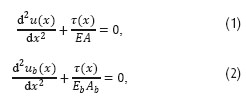
s neznámou u(x) resp. u_b(x) a τ(x), kde A resp. A_b je plocha příčného řezu kolejnice resp. mostu. Předcházející soustavu lze vyjádřit i v silách jako:

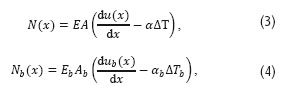
s neznámými u(x) resp. u_b(x) a N(x) resp. N_b(x). Je zřejmé, že v soustavě reprezentované rovnicemi (1) a (2) je příliš mnoho neznámých a proto je třeba přijmou další předpoklad. Podélné smykové síly na styku kolejnice a mostu jsou proto uvažovány jako lineární funkce vzájemných posunů mostu a kolejnice dle rovnice:

τ(x) = k(u_b(x) - u(x))      (5)

kde k představuje měrný odpor proti podélnému posunutí kolejnice vůči mostu v [N·m^–2] (Pozor, nezaměňovat s podélným odporem proti posunutí k_p, používaným v teorii bezstykové koleje, který má jednotky [N·m^–1].) Je dobré si uvědomit, že konstanta k reprezentuje součet všech dílčích měrných odporů, které se mezi kolejnicí a mostem nacházejí (tzn. odpor proti posunutí v kolejovém loži, odpor proti posunutí v upevnění, vůli resp. odpor jednotlivých dílů upevnění atd.).

Podélná tuhost mostu (součin E_bA_b) je výrazně větší než podélná tuhost kolejnice (EA). Vzhledem ke skutečnému rozdílu mezi průřezovou plochou kolejnice a mostu, není předpoklad realitě příliš vzdálen. Uvažujeme:

E_bA_b >> EA      (6)

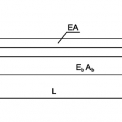
Pro řešení soustavy (1) a (2) s předpoklady (5) a (6) je třeba správně stanovit okrajové podmínky. Zvolené podmínky jsou dobře patrné z obr. 2.

Zkoumaná mostní konstrukce je spojitý nosník o dvanácti polích s pevným krajním ložiskem. Posunu mostu je tedy v tomto místě zabráněno, proto:

u_b(0) = 0      (7)

Všechna ostatní ložiska mostu jsou posuvná, a tedy mostu umožňují dilatovat. Na pravém konci mostu tak neočekáváme žádné normálové napětí (a z něj pocházející sílu), neboť při tomto uspořádání podpěr most dle principu minima celkové energie dilatuje právě tak, aby v něm žádné napětí nevzniklo. Na pravém konci mostu bude tedy:

N_b(L) = 0      (8)

kde L reprezentuje délku mostu.

Podobné okrajové podmínky jako pro most lze předepsat i pro kolejnici. Na pravém okraji mostu je umístěno dilatační kolejové zařízení (KVVDZ), které umožňuje kolejnici podélný posun jejího konce. Na pravém konci mostu je tedy:

N(L) = 0      (9)

Protože délka mostu je značná a převyšuje obvyklou délku dýchajícího konce, na levém konci mostu je uvažována bezstyková kolej s tzv. plným napětím. Tato úvaha vede na okrajovou podmínku ve tvaru:

u(0) = 0      (10)

Uvážení okrajových podmínek (7) až (10) a předpoklad, že součinitel tepelné roztažnosti mostu je totožný se součinitelem teplotní roztažnosti kolejnice (α = α_b) vede na řešení:

u_b(x, ΔT_b) = αΔT_bx      (11)

pro posun mostu a:

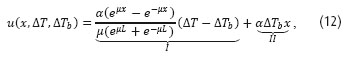
pro posun kolejnice.

Z rovnice (11) lze vyčíst, že most může v podstatě volně teplotně dilatovat, což je v souladu nejenom s naším fyzikálním názorem, ale i se skutečností, že vliv spolupůsobení kolejnice na most (nikoli ovšem naopak) jsme zanedbali (viz rovnici (6)).

Ze struktury rovnice (12) je dobře vidět, že celkový posun kolejnice v libovolném místě je součtem posunu mostu (v rovnici (12) vyjádřený svorkou II. Povšimněme si, že zcela odpovídá u_b dle rovnice (11)), který logicky závisí na teplotě mostu ΔT_b a dále částí označenou svorkou I, která reprezentuje spolupůsobení mostu a kolejnice a závisí na rozdílu teplot kolejnice a mostu (ΔT-ΔT_b).

Statistické vyhodnocení měření
Z teoretické přípravy, která nás dovedla k rovnici (12) vidíme, že posunutí pravého (volného) konce kolejnice je lineární kombinací vlivu rozdílu rovnoměrné změny teploty kolejnice a mostu (ΔT-ΔT_b) a rovnoměrné změny teploty mostu ΔT_b. Zároveň vidíme, že v rovnici (12) se nevyskytuje absolutní člen. To je vcelku v souladu s  očekáváním, kdy při nulové změně teploty přirozeně očekáváme i nulový posun mostu a kolejnice vlivem této změny. Pro tyto případy má statistika připraven postup lineární regresní analýzy bez absolutního členu, který je zde využit.

Za předpokladu nezávislosti a normálního rozložení vstupních veličin lze řešený problém zapsat ve tvaru:

Y_i = β₁X_i1 + β₂X_i2 + ... + β_jX_ij      (13)
i = 1,2...n, j = 1,2

kde Y_i je sledovaná proměnná – posunutí volného konce kolejnice u, X_ij jsou hodnoty vysvětlujících proměnných – rozdíl teplot kolejnice a mostu (ΔT-ΔT_b) a změna teploty mostu ΔT_b, bj jsou hledané koeficienty lineární regrese, n představuje počet měření. Pomocí statistických postupů můžeme určit koeficienty bj a z nich následně
hodnotu měrného odporu proti posunutí:

k = 79,939 [kN·m^-2]      (14)

V číselném řešení byly uvažovány následující hodnoty konstant:

délka mostu L=  439,000 [m],
Youngův modul pružnosti ocele E = 210 · 109 [Pa],
příčný průřez kolejnice 60 E1 (UIC 60) A = 72,86 · 10–4 [m²].

Interpretace výsledků
Z naměřených dat (teploty mostu, teploty kolejnice a posunutí kolejnice na jejím volném konci) byla spočtena hodnota měrného odporu proti posunutí kolejnice vůči mostu (viz (14)).

Spočtená hodnota k je ovšem nesouměřitelná (jak jednotkami, tak fyzikální podstatou) s běžně používanou hodnotou odporu proti posunutí kolejnice v upevnění. Pro interpretaci výsledků jsou dále uvedeny následující grafy.

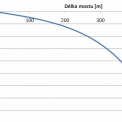
Na obr. 3 je vynesena působící podélná smyková sílaτ [kN·m^–1] při pevně zvolené kombinaci teplot ΔT = 16 °C a ΔT_b = 5 °C v závislosti na délce mostu.

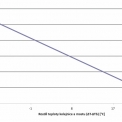
V obr. 4 je vynesena celková smyková síla mezi kolejnicovým pásem a konstrukcí N_τ při pevně zvolené základní teplotě T_b = 10 °C (ΔT_b = 0 °C) v závislosti na změně teploty kolejnice T v rozmezí 0 až 35 °C (ΔT Ε <–10;+25> °C).

SHRNUTÍ A ZÁVĚR
Celkové výsledky praktických měření i teoretické analýzy chování mostní konstrukce a kolejnice ukazují následující:

• ke vzájemnému pohybu kolejového roštu a mostní konstrukce při změně klimatických podmínek nedochází,
• nepřesnosti výpočtu lze přisoudit zjednodušení náhradní modelové konstrukce, která byla oproti skutečnosti modelována jako přímá, a měření teploty mostní konstrukce, která byla měřena na povrchu a není ve skutečnosti konstantní v celé délce,
• uvedený výpočtový model dává uspokojivé výsledky pro stanovení celkové smykové síly mezi kolejovým pásem a konstrukcí v místě MZ,
• výpočet lze aplikovat na stanovení maximálního posunu v KVVDZ s vyhovující technickou přesností.

Do budoucna je možné výpočet zlepšit ve dvou oblastech:

• v oblasti měření by bylo vhodné teplotu mostní konstrukce sledovat ve více místech na mostě a nikoli na povrchu mostní konstrukce, ale uvnitř (nejlépe kontinuálním měřením),
• v oblasti matematického modelu by bylo vhodné zohlednit skutečné zakřivení mostní konstrukce (vede na 2D anebo 3D model), zvětšenou tuhost v oblasti pevné podpory (kolejové rozvětvení st. Praha hl. n.) a zavést model s přesněji popsaným spolupůsobením mezi kolejnicovým pásem a konstrukcí mostu.

LITERATURA:
[1] Esveld, C: Modern Railway Track. Second edition; MRT-Production, 2001
[2] Jarušková, D.: Pravděpodobnost a matematická statistika. Dotisk druhého vydání; skripta ČVUT, 2009
[3] Krejčiříková, H.: Zkušenosti s dilatačními zařízeními na dlouhých mostech, Nová železniční technika 2011, roč. 19, č. 2, s. 18-22. ISSN 1210-3942

Behaviour of continuous welded rail in bridge expansion joint
Behaviour of continuous welded rail in interaction with bridges constructions represents one of the main problems in modern railway construction, especially on bridges longer than 200 m. Bridge over Masaryk Railway Station (which is part of the New Connection) in Prague is such a bridge. During 2008 to 2012 as part of MŠMT 6840770001 project, measurement was carried out on that bridge, collecting data about the position of rail according to rails and bridges temperature. Evaluation procedure of that data and computed results from measurement are presented in this article.

Autoři

• Bc. Pýcha Marek
• doc. Krejčiříková Hana CSc.